PCMレク：Lesson5,6,7

Contents

Lesson 5：Displaying Data in Public Health

公衆衛生（Public Health）におけるデータ表示（Displaying Data）

一般的な目標（General objectives）

  1. 表（tables）、グラフ（graphs）、チャート（charts）を利用した異なるデータの表現を理解する。
  2. 疫学（epidemiological）報告で使用される表、グラフ、チャートの異なる効用を解釈できるようになる。
  3. データ表示の異なる方法をいつ使用するかを決定する。
  4. 実際の疫学調査（epidemiological survey）で一般的なデータ表示方法を適用する。

概要（Overview）

  • データ分析（Data analysis）は公衆衛生実践の重要な要素です。データを調査する際には、適切な表示フォーマットを選択するために最初にデータタイプを特定する必要があります。
  • データを効果的に分析するためには、分析技術を適用する前にデータに慣れることが必要です。疫学者/研究者は、個別記録（line listing）を含むようなものから調査を始めることができます。
  • 時には、結果として得られる表が必要な唯一の分析であることもあります。特にデータ量が少なく関係が直接的な場合はそうです。
  • データがより複雑な場合、グラフとチャートはより広範なパターンや傾向を視覚化し、それらの傾向からの変動を特定できるようになります。データの変動は重要な新しい発見を代表するか、または入力またはコーディングの誤りを表しているかもしれません。これらの誤りは訂正される必要があります。したがって、表とグラフはデータの検証と分析を支援する有用なツールとなり得ます。
  • 分析が完了すると、表とグラフは他の人にデータを説明するための有用な視覚的補助としてさらに機能します。表とグラフを準備する際には、情報を伝えることが主な目的であることを念頭に置いてください。

表（Tables）

  • 表は、行と列に配置されたデータのセットです。
  • ほとんどの量的情報は表に組織化することができます。
  • 表はパターン、例外、違い、その他の関係を示すのに役立ちます。
  • 表は通常、データの追加の視覚的表示（グラフやチャートなど）を準備するための基盤として機能します。これらの表示ではいくつかの詳細が失われる場合があります。
    • 種類（Types）：
      • 一変数表（One-variable tables）
      • 二変数及び三変数表（Two- and three-variable tables）

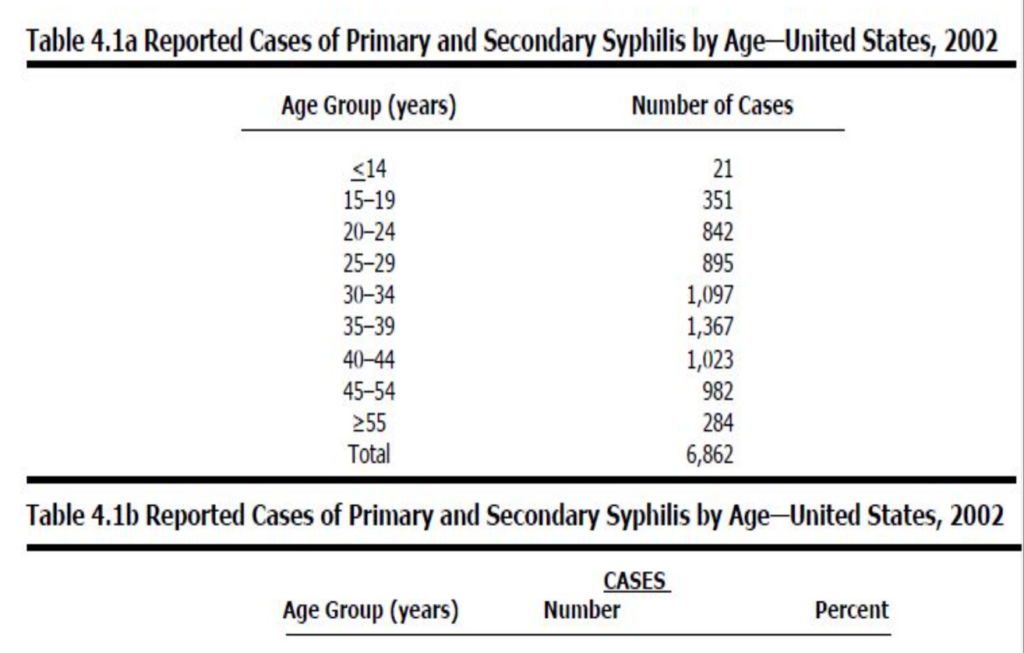
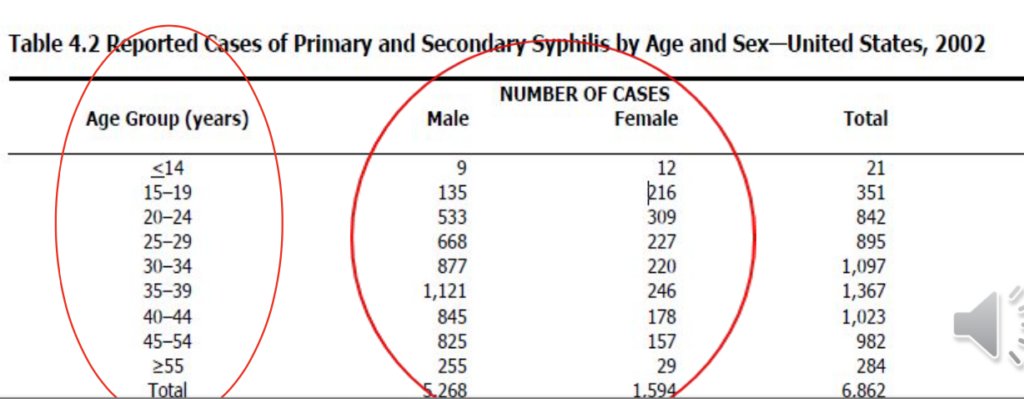
緊急表（Contingency table）

  • 二変数表であり、その二つの変数によって共同でデータが分類されます。
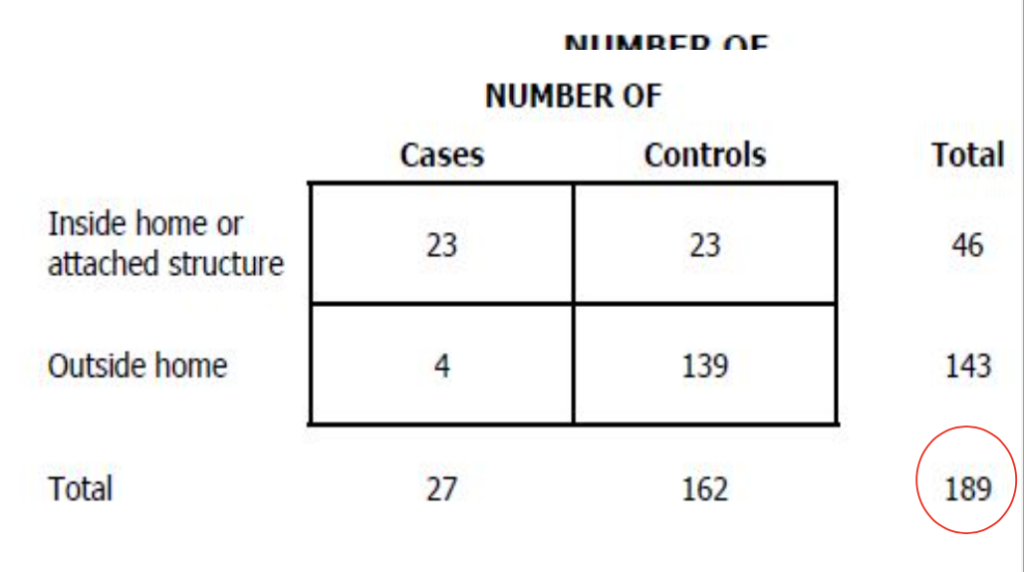
  • 2 x 2表は、露出のある者とない者、疾患のある者とない者を比較するのに便利です。露出と疾患の関係を評価することができます。
  • 2 x 2表は、各々の二つの変数が二つのカテゴリを持つ特殊な種類の緊急表の一例です。
  • 2 x 2表変数：露出変数（Exposure variable）と結果変数（Outcome variable）。

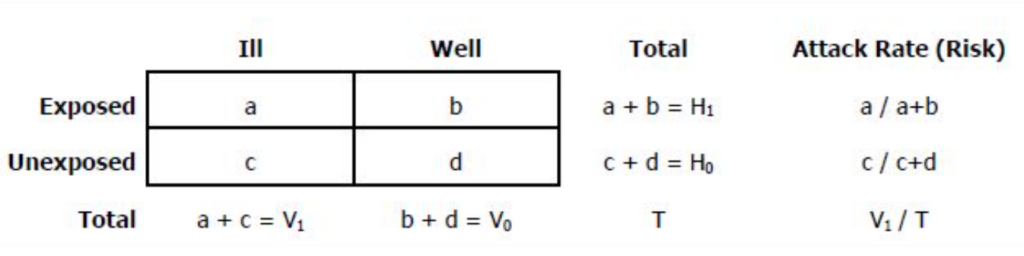
2×2表を使用した攻撃率の計算（Calculation of Attack rate using 2×2 table）

  • H1とH0はそれぞれ露出した人と露出していない人の総数を表します。
  • 「Vi」は縦の合計を表し、V1とV0はそれぞれ病気の人と健康な人（または症例と対照）の総数を表します。
  • 2×2表に含まれる被験者の総数は、文字T（またはN）によって表されます。

頻度以外の統計量の表（Tables of statistical measures other than frequency）

  • 頻度（frequency）以外にも、表のセルは平均値、率、相対リスク（relative risks）、または他の疫学的（epidemiological）測定値を表示することもあります。

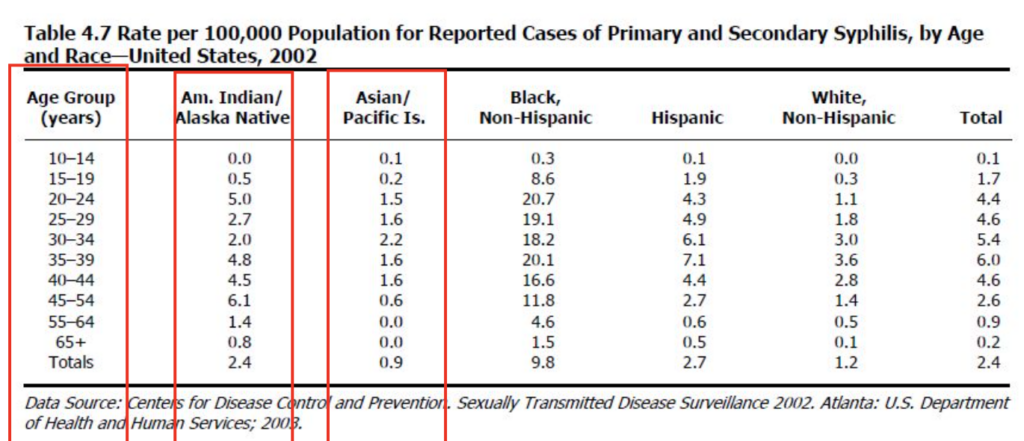
複合表（Composite tables）

  • レポートや原稿でスペースを節約するために、複数の表を一つに組み合わせることがあります。
  • この種の表は三方向表（three-way table）として解釈されるべきではないことを認識することが重要です。
  • 変数は関係を示しません。
  • 純粋に、複数の一変数表（各変数による症例数を個別に評価する）がスペースを節約するために連結されています。

表のシェル（Table shells）

  • 研究が行われる前に書かれるほとんどのプロトコルでは、データがどのように分析されるかについての記述が必要です。
  • データを収集する前にデータを分析することはできませんが、研究が何を伝えるかを明確にし、データが収集された後の分析を迅速化するために、あらかじめその分析を予測して設計します。

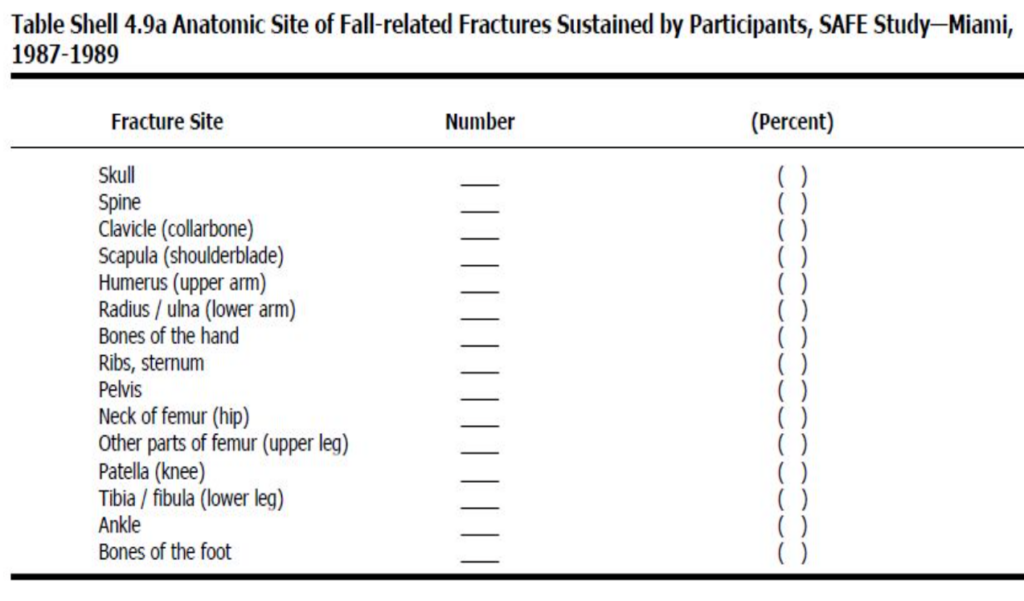
階級区間の作成（Creating class intervals）

  • 階級区間は、可能な応答の範囲が広い関連変数を体系的に分類する方法です。
  • 階級区間が年齢である場合、年齢範囲は重複しないようにすべきです。ほとんどの測定は従来の丸めルールに従います。
  • カテゴリを構築する際には生物学的妥当性（biologic plausibility）の原則を使用します。
  • 初期分析のためには多くの階級区間を使用して、データの変動性を把握します。
  • 自然な基線群（baseline group）は独自のカテゴリとして保持されるべきです。しばしば、基線群は露出がない者、例えば非喫煙者（1日0本のタバコ）を含みます。

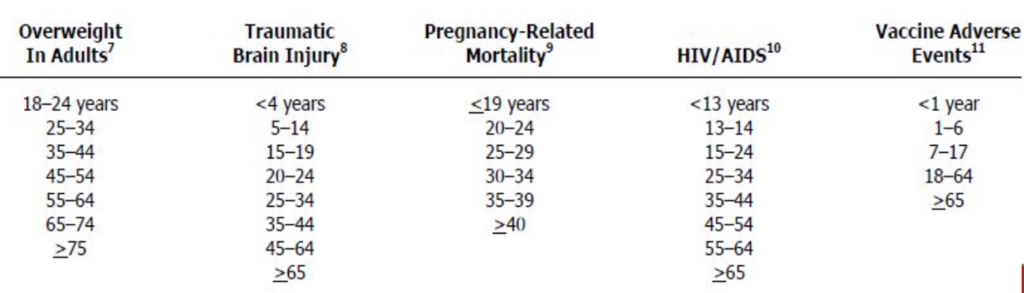
階級区間の作成に関するガイドライン（Guidelines for creating class intervals）

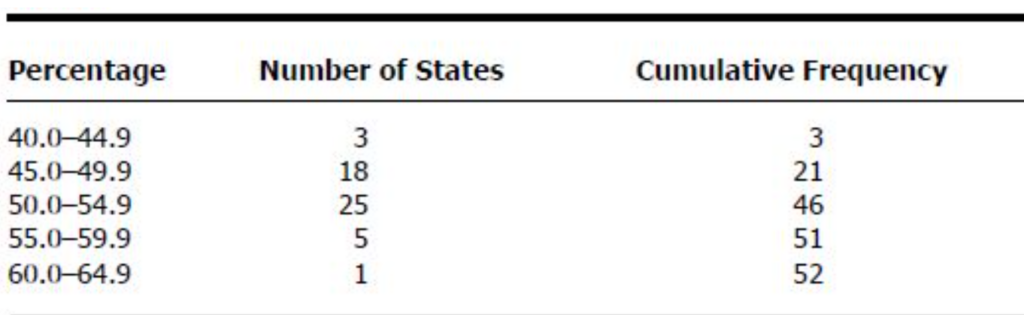
戦略1：データを同様のサイズのグループに分ける（Strategy 1: Divide the data into groups of similar size）

  • 州（Location）による症例の発生率を示す。
  • スポットマップ（spot maps）を作成するのに役立ちます。
  • 観測数が同じになるように間隔を設定します。

戦略2：平均値と標準偏差に基づいて区間を設定する（Strategy 2: Base intervals on mean and standard deviation）

  • 分布の平均値と標準偏差を計算します。
  • この戦略は大規模なデータセットに最も適しています。

戦略3：範囲を等しい階級区間に分ける（Strategy 3: Divide the range into equal class intervals）

  • この方法は最もシンプルで一般的に使用され、グラフに最も容易に適応できます。
  • データセットの値の範囲を見つけます。つまり、最大値（またはやや大きい便利な値）とゼロ（または最小値）の差を見つけます。
  • 何個の階級区間（グループまたはカテゴリ）を持ちたいか決めます。
  • 表では四つから八つの階級区間を選びます。
  • グラフやマップでは三つから六つの階級区間を選びます。
  • 数は、データのどの側面を強調したいかに依存します。

グラフ（Graphs）

  • 数値データを視覚形式で表示します。データのパターン、傾向、異常、類似点、および表では明らかでないかもしれないデータの違いを示すことができます。
  • グラフは、データを分析し、データの意味を理解しようとする際に不可欠なツールです。
  • 水平軸はx軸と呼ばれ、通常は独立変数（independent variable、またはx変数）である時間や年齢層などの値を示します。
  • 垂直軸はy軸と呼ばれ、依存変数（dependent variable、またはy変数）である症例数や疾病率などの頻度測定を示します。

算術スケール折れ線グラフ（Arithmetic-scale line graphs）

  • 時間などの変数に沿った傾向やパターンを示します。
  • 疫学では、このタイプのグラフは長期間にわたるデータシリーズを示し、複数のシリーズを比較するために使用されます。
  • Y軸の目盛間隔は連続変数を、X軸の目盛間隔は離散変数を表します。
  • これらのグラフは主に時間を通じての全体的な傾向を描写するために使用され、特定の観測（単一データポイント）の分析よりも重視されます。

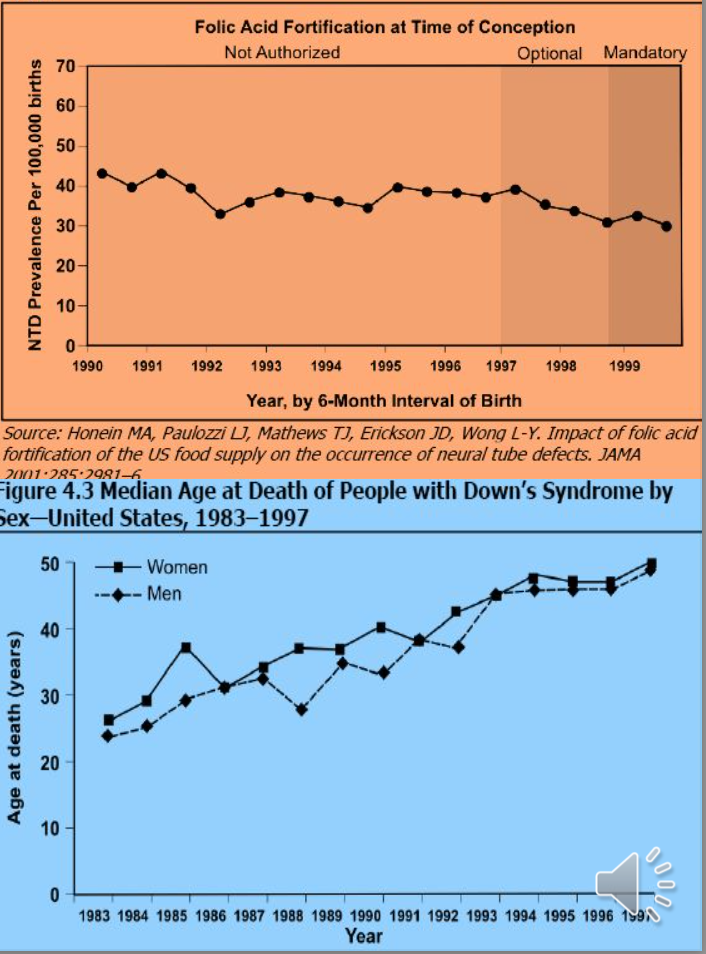
半対数スケール折れ線グラフ（Semi-logarithmic-scale line graphs）

  • 算術グラフだけでは不十分な競合力を描写するために使用され、問題のある年を強調するためのインセットが必要な場合に利用されます。
  • この「半対数」グラフは、幅広い値の範囲を持つ変数を表示する際に有用です。
  • 複数のシリーズの相対的な変化率を示すのにも使用されます。算術スケール折れ線グラフ上の直線は数または量の一定の変化を表し、半対数スケール折れ線グラフ上の直線は一定の割合の変化を表します。

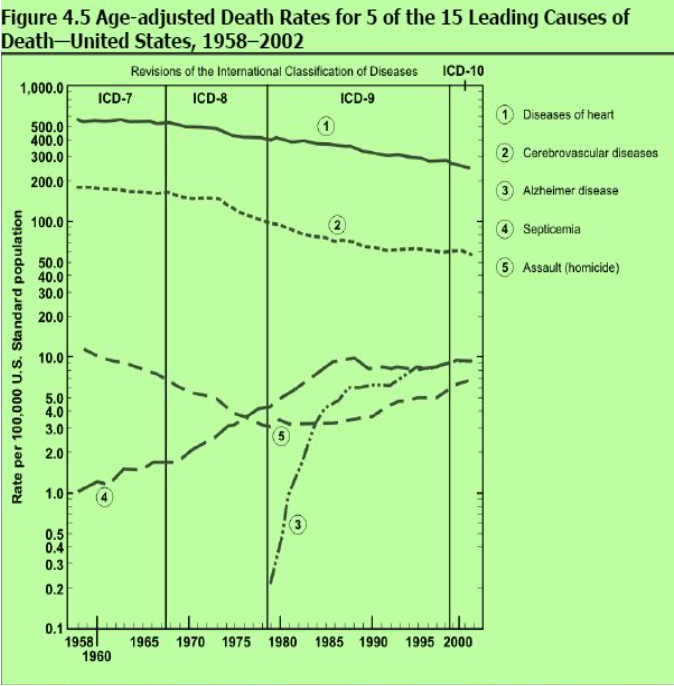
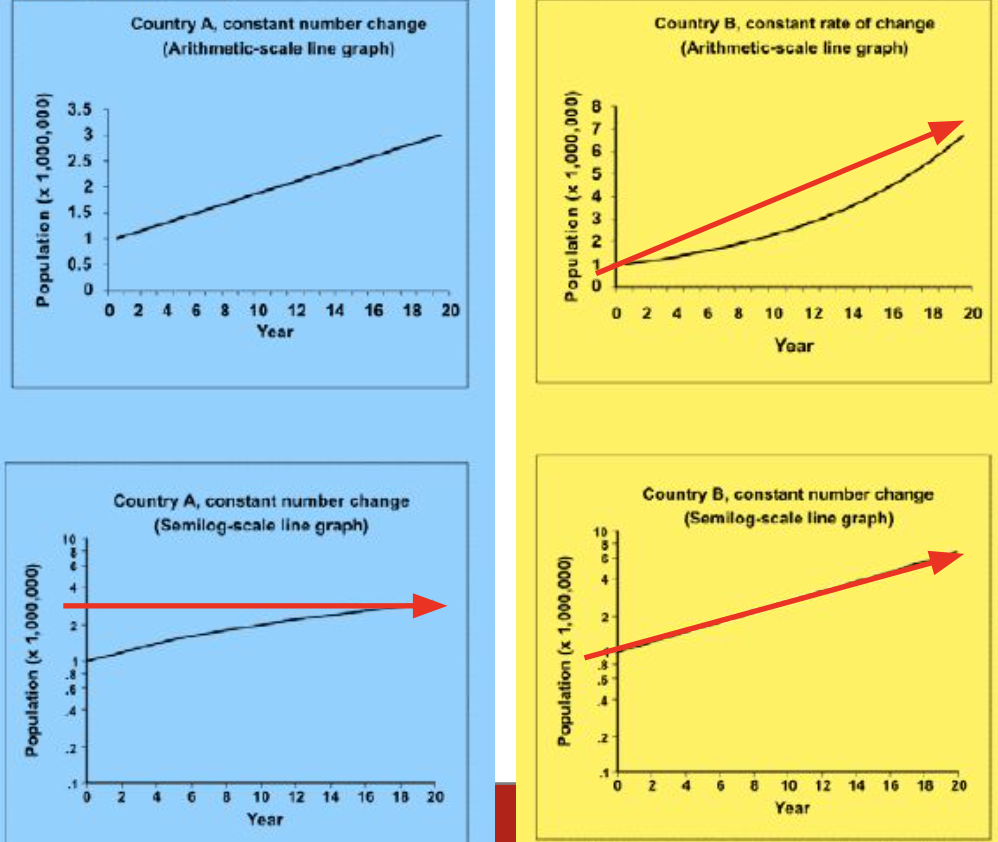
算術スケール折れ線グラフ vs 半対数スケール折れ線グラフ（Arithmetic-scale line graphs vs Semi-logarithmic-scale line graphs）

  • これら二つのグラフタイプの違いを理解することは、データの分析と解釈において重要です。算術スケール折れ線グラフは通常の値の変動を表すのに適している一方で、半対数スケール折れ線グラフは変化率が重要な場合に有効です。

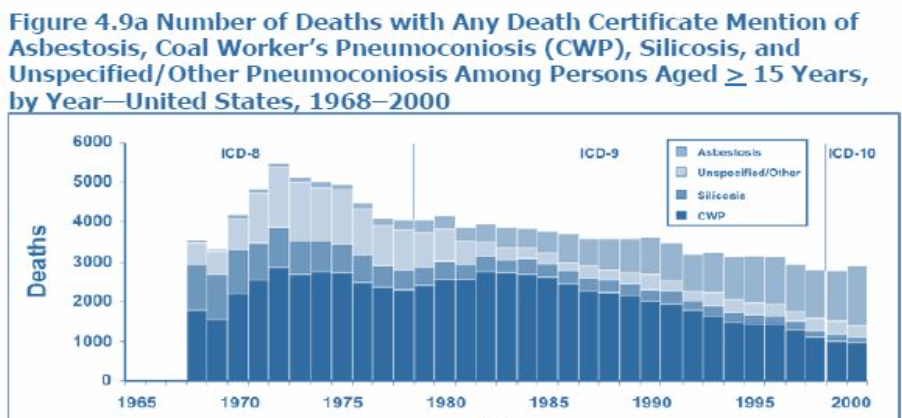
ヒストグラム（Histograms）

  • ヒストグラムは、連続変数の頻度分布のグラフで、階級区間に基づいています。
  • 隣接する列を使用して、分布内の各階級区間の観測数を表します。
  • 各列の面積はその区間の観測数に比例します。
  • ヒストグラムで全ての階級区間が等しい場合、各列の高さはそれが表す観測数に比例します。
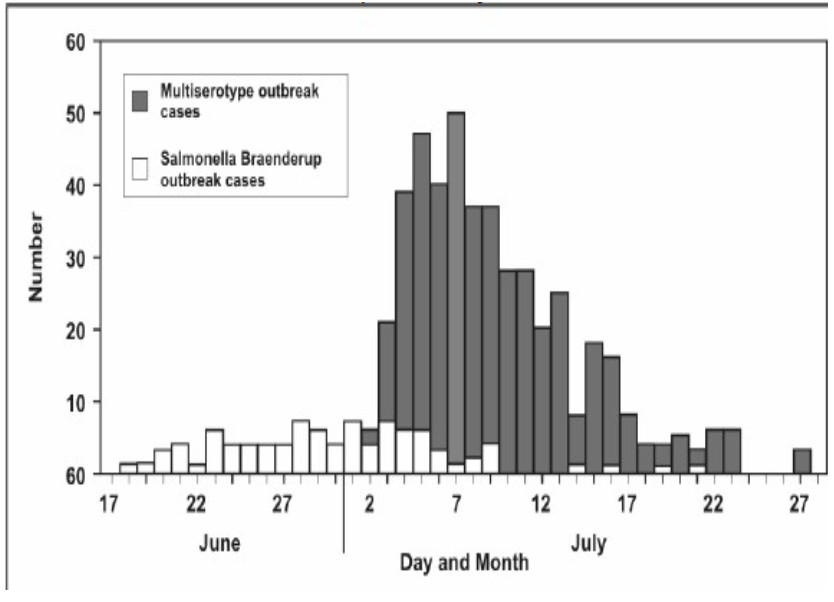
  • 流行曲線（epidemic curve）はヒストグラムの特殊なタイプで、発症時または診断時の疾患の症例数を時間によって表示します。

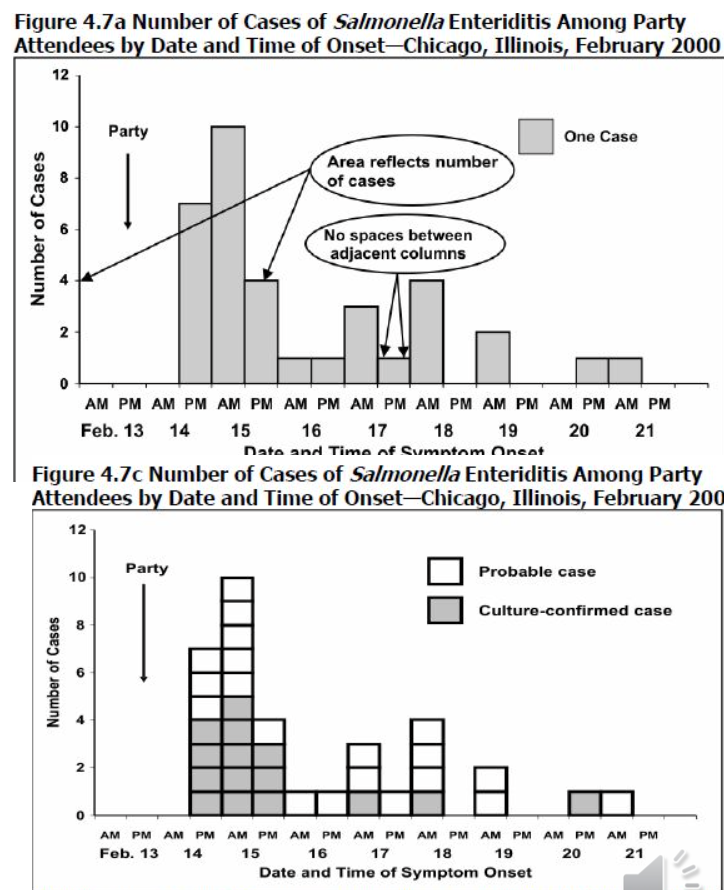
人口ピラミッド（Population pyramid）

  • 人口ピラミッドは年齢と性別による人口の数または割合を表示します。
  • ヒストグラムを使用して、症例数や頻度の大きさまたは数を示します。
  • 人口ピラミッドは通常、国の人口分布を表示するために使用されますが、疾病や健康特性など、他のデータを年齢と性別によって表示するためにも使用されます。

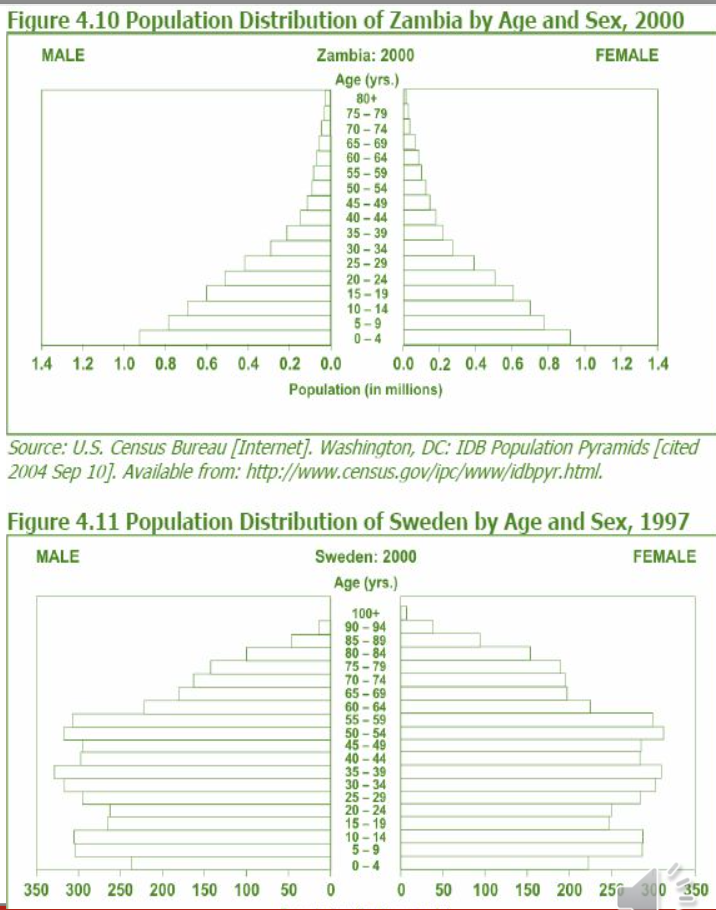
頻度多角形（Frequency polygons）

  • 頻度多角形は、ヒストグラムのように、頻度分布のグラフです。
  • 区間内の観測数は区間の中点に位置する単一の点でマークされます。
  • 各点は次の点と直線で接続されます。
  • 頻度多角形は、同じデータのヒストグラムと同様に、曲線の下の領域を含んでいます。
  • 頻度多角形（またはヒストグラム）は、連続変数の全頻度分布（カウント）を表示するために使用されます。
  • 算術スケール折れ線グラフは、通常、時間を通じて観察されたデータポイント（カウントまたは率）の一連をプロットするために使用されます。頻度多角形は両端を閉じる必要がありますが、算術スケール折れ線グラフは単にデータポイントをプロットします。

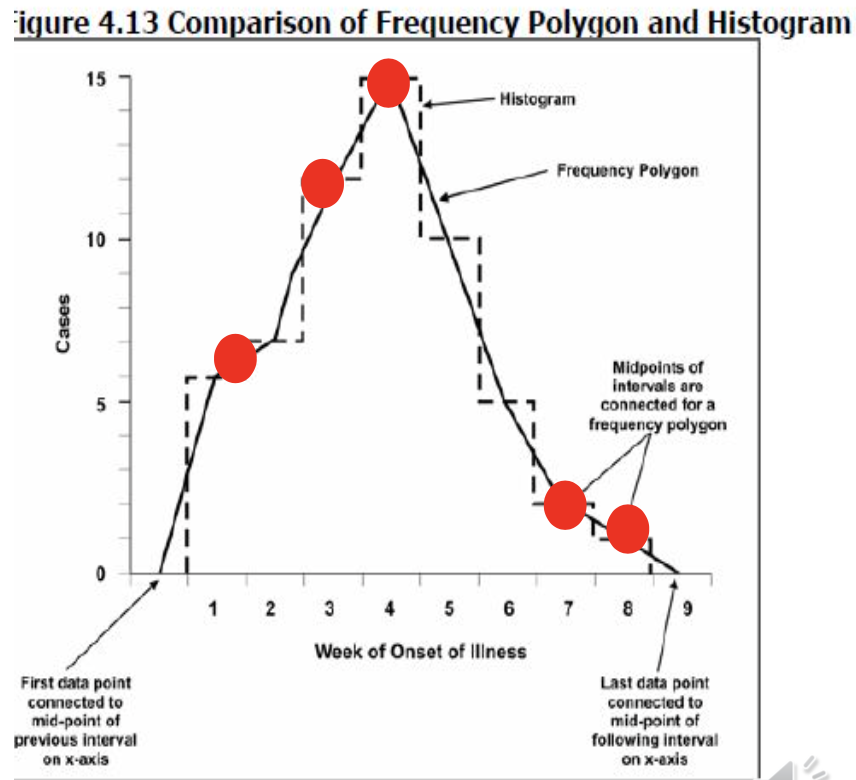
散布図（Scatter diagrams）

  • 散布図（または「散布グラム」）は、二つの連続変数間の関係を示すグラフで、x軸が一つの変数を、y軸がもう一つの変数を表します。
  • 左上から右下へのコンパクトなパターンは負または逆の相関を示し、一方の変数が増加するにつれて他方の変数が減少します。
  • 点が広く散らばっているか、比較的平らなパターンは、相関がほとんどないことを示します。

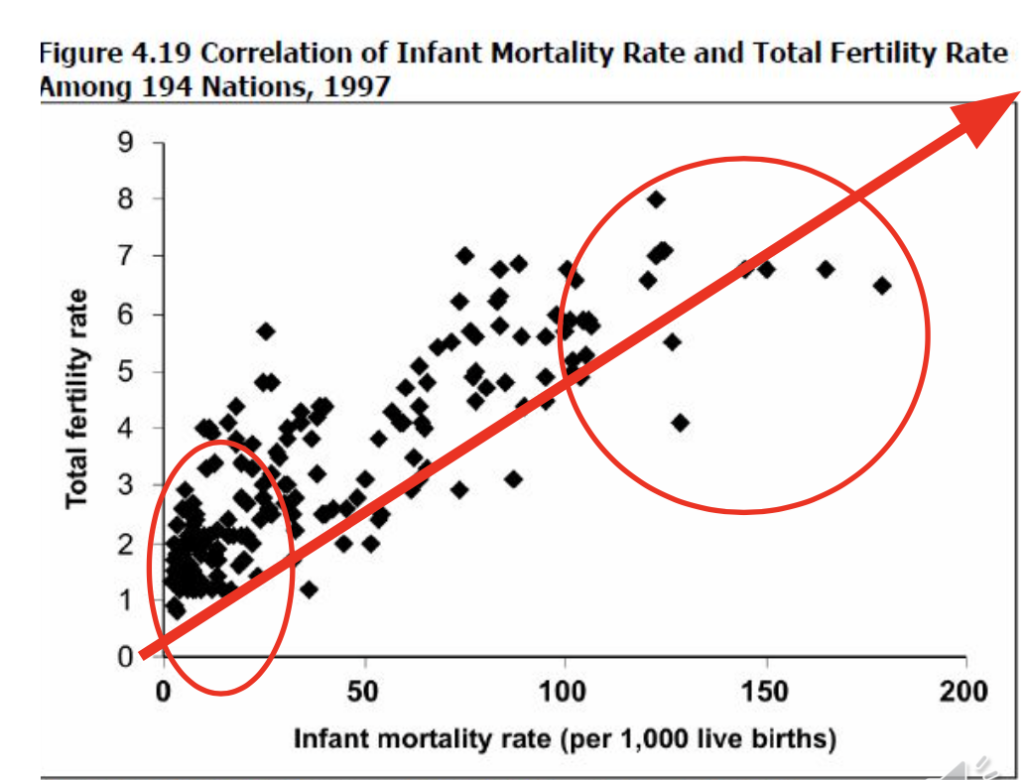
棒グラフ（Bar charts）

  • 棒グラフは等幅の棒を使用して比較データを表示します。
  • カテゴリ間の比較は、そのカテゴリのイベントの頻度に比例する棒の長さに基づいています。
  • 異なるカテゴリの棒は空間によって区切られます（ヒストグラムの棒とは異なります）。
  • 棒グラフは、棒を縦または横に配置して描画することができます。
  • 棒は通常、昇順または降順の長さ、またはカテゴリの本質的な順序に基づいた他の体系的な順序で配置されます。
  • 棒グラフに適したデータには離散データが含まれます。

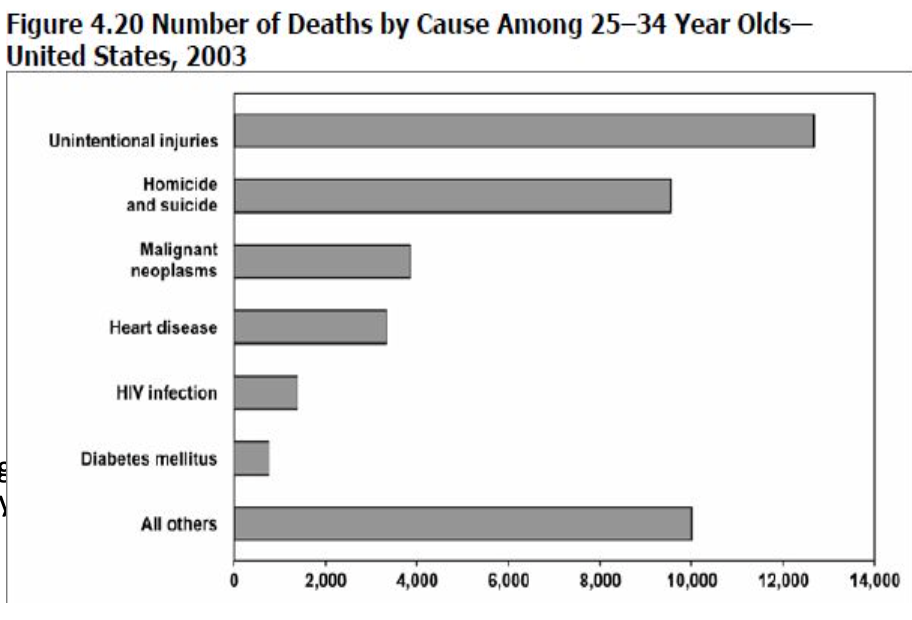
群棒グラフ（Grouped bar charts）

  • 群棒グラフは二変数または三変数表からのデータを示すために使用されます。
  • 群棒グラフは、グループ内のサブグループを比較する場合に特に有効です。グループ内の棒は隣接しています。
  • このグラフは、同じ年の死因の違いを示すのには効果的ですが、単一の原因の年間違いを示すのにはあまり効果的ではありません。
  • 図の目的が二つの年間の特定の原因を比較する場合には、それに応じて設計される必要があります。

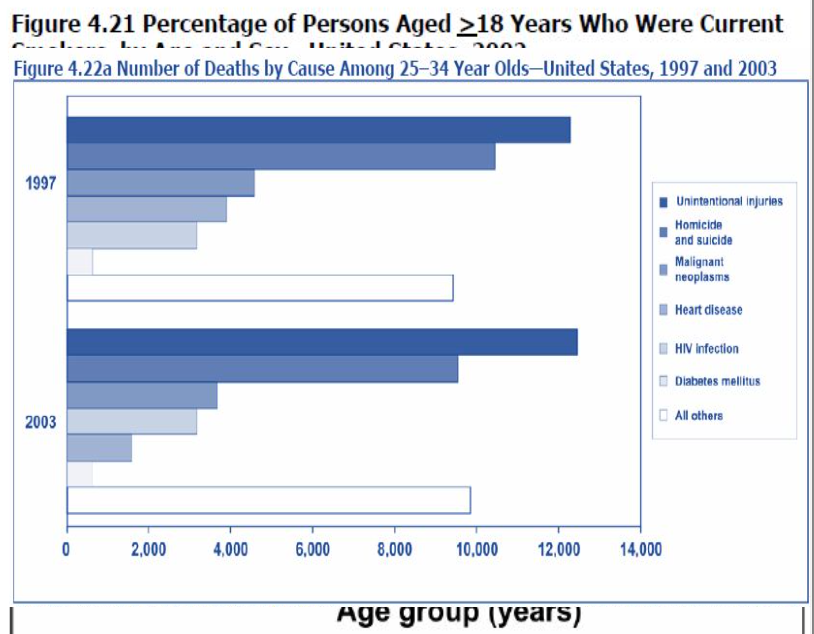
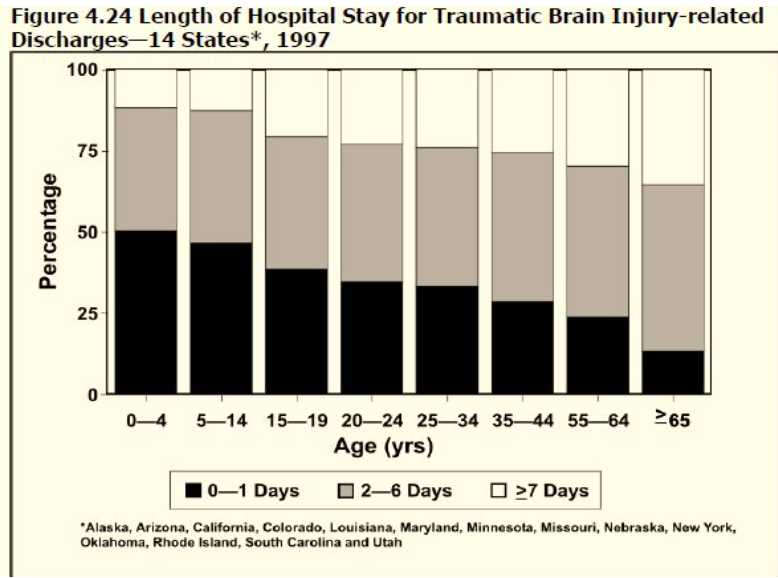
積み上げ棒グラフ（Stacked bar charts）

  • 積み上げ棒グラフは群棒グラフと同じデータを示しますが、第二変数のサブグループを第一変数の単一の棒内の異なるセグメントとして積み上げます。
  • 積み上げ棒グラフは、群棒グラフとは異なり、異なるグループを別々の棒ではなく、各カテゴリの単一の棒内の異なるセグメントで区別します。
  • 第一変数の全体的なパターンを表示するのには群棒グラフよりも効果的ですが、各サブグループの相対的なサイズを表示するのには効果的ではありません。
  • 積み上げ棒グラフは、第一変数の全体的なパターンを表示するのに群棒グラフよりも効果的であり、一方で各サブグループの相対的なサイズを表示するのには効果的ではありません。これは、異なるサブグループが一つの棒内で積み重ねられるため、個々のサブグループの比較が直感的でなくなるためです。

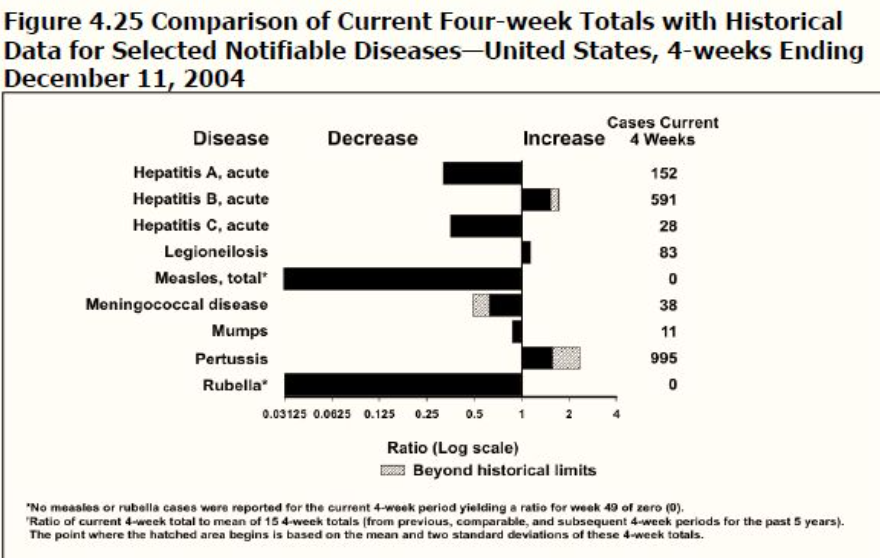
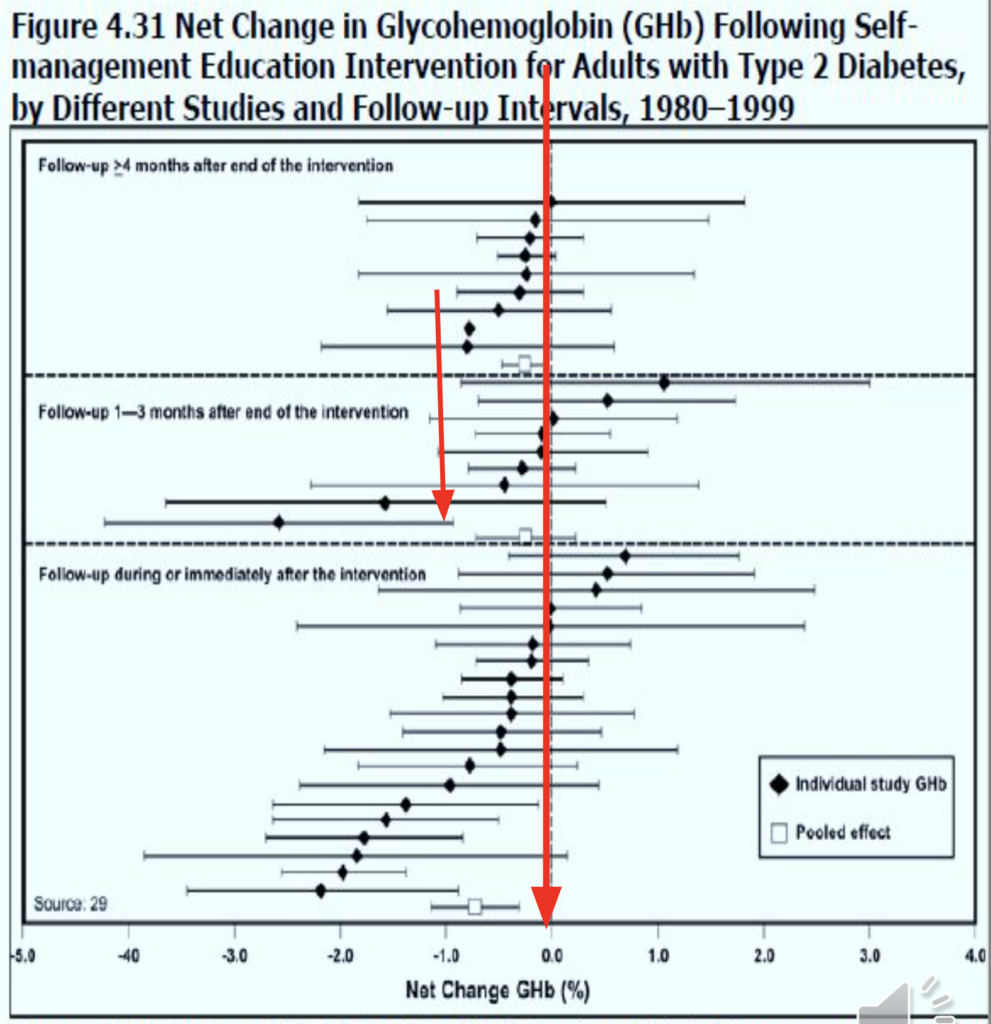
偏差棒グラフ（Deviation bar charts）

  • 偏差棒グラフは、ベースラインからの正と負の変更を表示します。
  • 歴史的な限界を超える値（95％信頼限界と比較可能）は、特別な注意を必要とするため強調されます。
  • このタイプのグラフは、時間を通じての変化の方向と大きさを視覚的に示すことで、データの変動を明確に理解するのに役立ちます。

円グラフ（Pie charts）

  • 円グラフは、各コンポーネント部分の割合的な寄与を「スライス」または楔形の大きさで示す、シンプルで理解しやすいチャートです。
  • 円グラフは単一変数の頻度分布の比率を示すのに有用です。
  • 複数の円グラフは、100％コンポーネントバーチャートの代わりに使用されることがあり、つまり、比率分布の違いを表示するために使用されます。

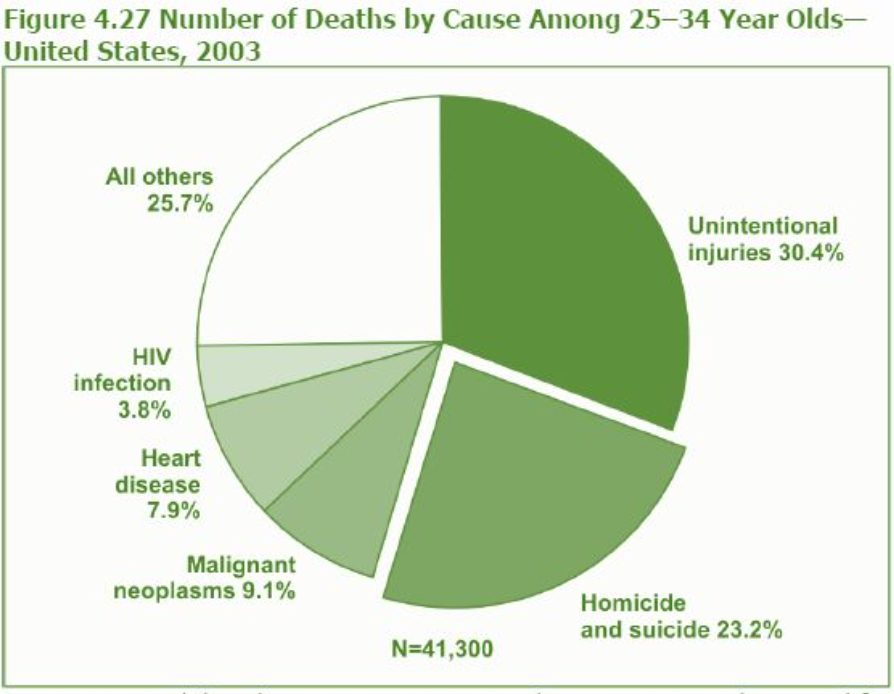
ドットプロットとボックスプロット（Dot plots and box plots）

  • ドットプロットはドットを使用して、x軸のカテゴリカル変数とy軸の連続変数との間の関係を示します。各観測に対して適切な場所にドットが配置されます。
  • ドットプロットは、x軸変数の各カテゴリでの観測のクラスタリングと広がりだけでなく、カテゴリ間のパターンの違いも表示します。
  • 「ボックス」はデータポイントの中央50％（または四分位範囲）の値を表し、「ホイスカー」はデータが取る最小値と最大値まで伸びます。
  • 中央値はボックス内の水平線でマークされます。
  • ボックスプロットは、中央位置（中央値）、分散（四分位範囲と範囲）、および歪度（中央線がボックス内で中心にないことによって示される）を表示し比較するために使用することができます。

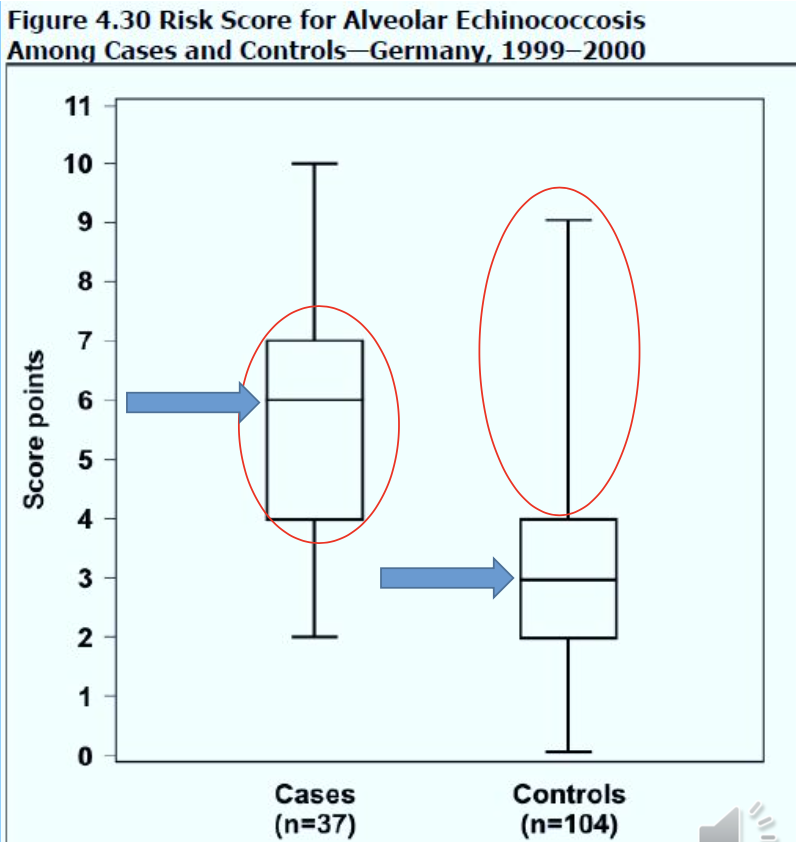
フォレストプロット（Forest plots）

  • メタ分析や体系的レビューのために個々の研究の点推定値と信頼区間を表示するために使用される、信頼区間プロット（Confidence interval plot）とも呼ばれます。
  • フォレストプロットでは、x軸は各研究からの主要なアウトカム測定（相対リスク、治療効果など）を表します。
  • 各研究は次のように表されます：
    • 水平線 — 信頼区間を反映
    • ドットまたは四角 — 研究のサイズやデザインの他の側面による点推定を反映
  • 水平線が短いほど、その研究の推定値の精度が高いことを示します。
  • 点推定（ドットまたは四角）が合理的に一列に並んでいる場合、研究が比較的一貫した効果を示していることを示します。
  • 垂直線はx軸上で効果がない（相対リスク = 1または治療効果 = 0）場所を示します。
  • 研究の水平線が垂直線を横切らない場合、その研究の結果は統計的に有意です。

まとめ（Summary）

  • 疫学的発見のメッセージを伝えるためには、最適なイラストレーション方法を選択する必要があります。
  • 表は一般的に数字、率、割合、累積パーセンテージを表示するために使用されます。
  • 表は情報を伝えることを意図しているため、ほとんどの表は二変数以下で、どの変数についてもカテゴリ（階級区間）は八つ以下であるべきです。
  • 表は名義または連続的順序データと一緒に使用することができます。性別や居住州のような名義変数は明確なカテゴリを持っています。
  • グラフはデータを迅速に視覚的に伝えることができます。算術スケール折れ線グラフは従来、時間を通じての疾病率の傾向を示すために使用されてきました。
  • 半対数スケール折れ線グラフは、疾病率が二桁以上の範囲で変動する場合に好まれます。
  • ヒストグラムと頻度多角形は頻度分布を表示するために使用されます。特別なタイプのヒストグラムである流行曲線は、流行期間中の発症時または診断時の症例数を表示します。
  • 単純な棒グラフと円グラフは単一変数の頻度分布を表示するために使用されます。群棒グラフと積み上げ棒グラフは二変数または三変数を表示することができます。
グラフ/チャートの種類使用時の目的
算術尺度折れ線グラフ（Arithmetic scale line graph）時間経過に伴う数値または割合のトレンドを示す（Show trends in numbers or rates over time）
半対数尺度折れ線グラフ（Semilogarithmic scale line graph）時間経過に伴う変化率を表示；2桁以上の範囲の値に適している（Display rate of change over time; appropriate for values ranging over more than 2 orders of magnitude）
ヒストグラム（Histogram）連続変数の頻度分布を示す；例えば、流行期間中の症例数やより長期間にわたる症例数（Show frequency distribution of continuous variable; for example, number of cases during epidemic or over longer period of time）
頻度多角形（Frequency polygon）連続変数の頻度分布を示す、特に成分を表示する場合に（Show frequency distribution of continuous variable, especially to show components）
累積頻度（Cumulative frequency）連続変数の累積頻度を表示する（Display cumulative frequency for continuous variables）
散布図（Scatter diagram）二つの変数間の関連をプロットする（Plot association between two variables）
単純棒グラフ（Simple bar chart）単一変数の異なるカテゴリのサイズまたは頻度を比較する（Compare size or frequency of different categories of a single variable）
群棒グラフ（Grouped bar chart）2から4のデータシリーズの異なるカテゴリのサイズまたは頻度を比較する（Compare size or frequency of different categories of 2 to 4 series of data）
積み上げ棒グラフ（Stacked bar chart）異なるグループの合計とその合計の構成部分を比較する（Compare totals and illustrate component parts of the total among different groups）
偏差棒グラフ（Deviation bar chart）ベースラインからの正および負の違いを示す（Illustrate differences, both positive and negative, from baseline）
100%構成棒グラフ（100% component bar chart）異なるグループで全体にどのように成分が寄与するかを比較する（Compare how components contribute to the whole in different groups）
円グラフ（Pie chart）全体の構成要素を示す（Show components of a whole）
スポットマップ（Spot map）事例やイベントの位置を示す（Show location of cases or events）
エリアマップ（Area map）地理的にイベントや割合を表示する（Display events or rates geographically）
箱ひげ図（Box plot）変数の分布の統計的特性（中央値、範囲、非対称性）を視覚化する（Visualize statistical characteristics (median, range, asymmetry) of a variable’s distribution）

Lesson 6：Summarizing data and Sampling (Variables, Frequency Distribution, Sampling in Public Health)

一般的な目標（General objectives）

  1. 異なるタイプの変数を定義し、決定する
  2. 中心位置（Central location）の尺度（モード（Mode）、メディアン（Median）、平均（Mean））を識別し、解釈する
  3. 頻度分布を構築する能力を持つ
  4. サンプリングの異なる方法を識別する

概要（Overview）

  • 研究者が全てのケースからデータを収集することは疑問があるため、サンプルを選択する必要があります。研究者がサンプルを抽出する全ケースのセットを人口（population）と呼びます。研究者は時間も資源もないため、ケースの数を減らすためにサンプリング技術（sampling technique）を適用します。
  • このモジュールでは、人口の中で露出されている、または露出に弱い人を識別する方法を学びます。また、その変動性に応じて人口の代表者を特徴づける方法も学びます。
  • 自然界で何かを測定する場合、通常は複数の測定を行う必要があります。これは物事が変動するためであり、状況を把握するためには複数の結果が必要です。これらの測定を行った後、何らかの方法でそれらを要約する必要があります。ほとんどの人にとって、数字の生データセットは解釈しにくいからです。

用語のレビュー（Review of Terms）

記述統計（Descriptive statistics）

  • データ値のセットを要約し説明するための統計ツールの使用
  • 人間は通常、数字または単語の長いリストから意味を作り出すのが難しい
  • 数字を要約するか、単語の出現を数えてその要約を単一の値で表現することが私たちにはより理解しやすい
  • 記述統計では、データセットやグループを比較する試みは行われません

推測統計（Inferential statistics）

  • 特定の要素を調査し、より大きな人口についての推論を行うことを可能にします
  • ここでは被験者や個人のグループを比較します
  • 通常、人口の全ての個体を研究に含めることはできませんが、統計を使用して得られた結果がより大きな人口に適用されると推測します。

人口（Population）

  • 少なくとも1つの共通特性を共有する個体のグループ
  • マクロレベルでは、これは人類全体を指すことがあります
  • 臨床研究のレベルでは、特定の病気やリスクファクターを持つすべての個体を指すことがありますが、それでも膨大な数の個体を意味することがあります
  • 非常に希少な状態の場合など、非常に小さな人口を持つことも十分に可能です
  • 研究の発見は、より大きな人口にその結果を推測するため、それらの研究結果に基づいて人口を管理するのに使用されます。

サンプル（Sample）

  • 人口内のメンバーの選択です。そのサンプルセットのメンバーを使用して研究が行われ、その結果はサンプルが取られた人口に推測されます
  • この統計分析の使用により、完全な人口を含めることが通常不可能であるため、臨床研究が可能になります。

パラメータ（Parameter）

  • 人口全体の値から計算される統計値をパラメータと呼びます。
  • 地球上のすべての個人の年齢を知って平均年齢を計算した場合、その年齢はパラメータになります。

変数（Variable）

  • 変数を定義する方法は多くありますが、研究のために収集された任意のデータ値のグループ名として変数を参照することができます。
  • 例には、年齢（age）、リスクファクターの存在（presence of risk factor）、入院時の体温（admission temperature）、感染症原因体（infective organism）、収縮期血圧（systolic blood pressure）が含まれます。
  • これは通常、データスプレッドシート（data spreadsheet）で列名（column names）となり、各行（row）が研究の個人の調査結果を表します。

データの整理（Organizing Data）

  • 変数は、身長（height）、性別（sex）、天然痘のワクチン接種状況（smallpox vaccination status）、身体活動パターン（physical activity pattern）など、人から人へ異なる任意の特性になり得ます。

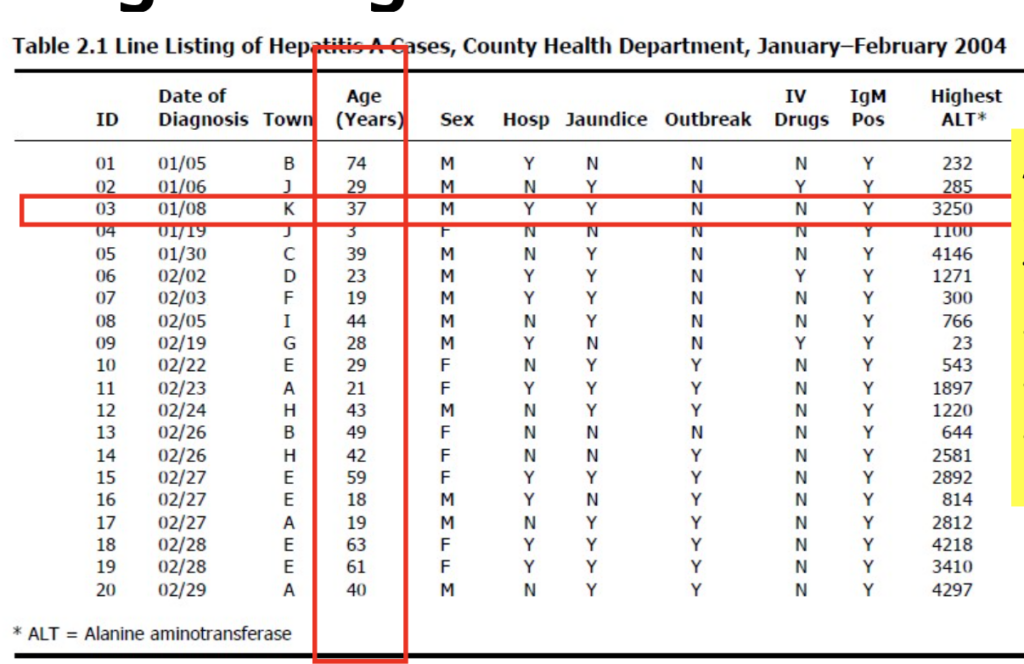
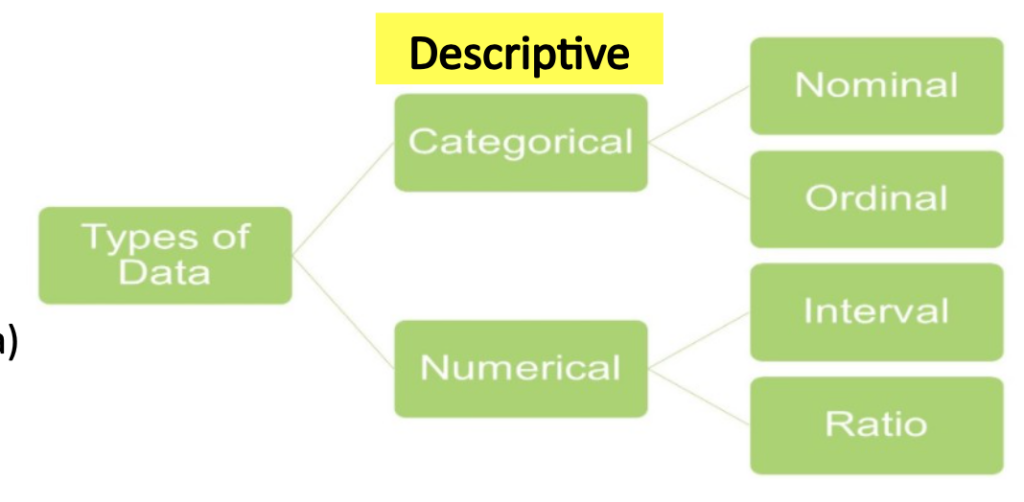
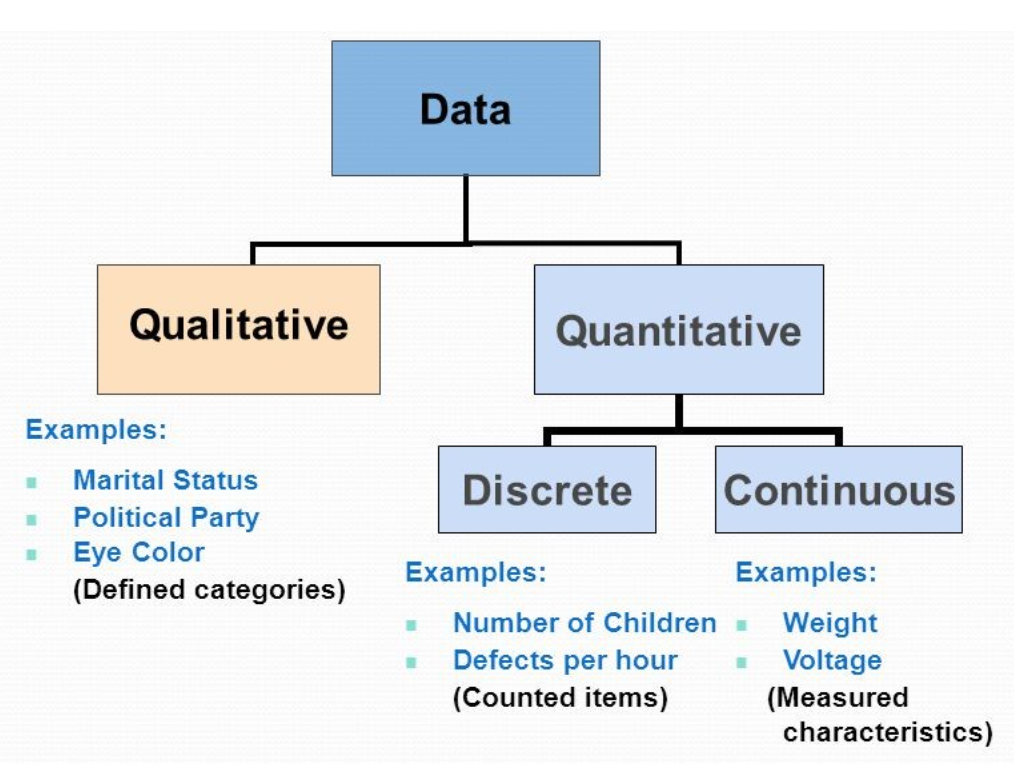
変数のタイプ（Types of Variables）

  • カテゴリカル（categorical）（名義（nominal）と順序（ordinal）データを含む）は、カテゴリや物事を指し、数値的な値ではありません。
  • 数値（numerical）（さらに、区間（interval）または比率（ratio）データとして定義される）は、測定とカウントに関するデータです。

名義尺度変数（Nominal-scale variable）

  • 値は数値的なランキングなしのカテゴリで、例えば居住県（county of residence）があります。
  • 疫学（epidemiology）では、生存（alive）か死亡（dead）、病気（ill）か健康（well）、ワクチン接種済み（vaccinated）か未接種（unvaccinated）、ポテトサラダを食べたか食べていない（did or did not eat the potato salad）など、2つのカテゴリのみを持つ名義変数が非常に一般的です。2つの相互に排他的なカテゴリを持つ名義変数は、時に二分変数（dichotomous variable）と呼ばれます。
  • 順序尺度変数（ordinal-scale variable）はランク付け可能な値を持ちますが、必ずしも均等に間隔があるわけではありません。例えば、がんの段階（stage of cancer）などがあります。
  • 区間尺度変数（interval-scale variable）は、真のゼロ点がないが、等間隔の単位で測定されます。例えば、生年月日（date of birth）などがあります。
  • 比率尺度変数（ratio-scale variable）は、真のゼロ点を持つ区間変数です。例としては、身長（height in centimeters）や病気の期間（duration of illness）があります。

頻度分布（Frequency Distributions）

  • 頻度分布は変数が取り得る値と、各値を持つ個人または記録の数を表示します。

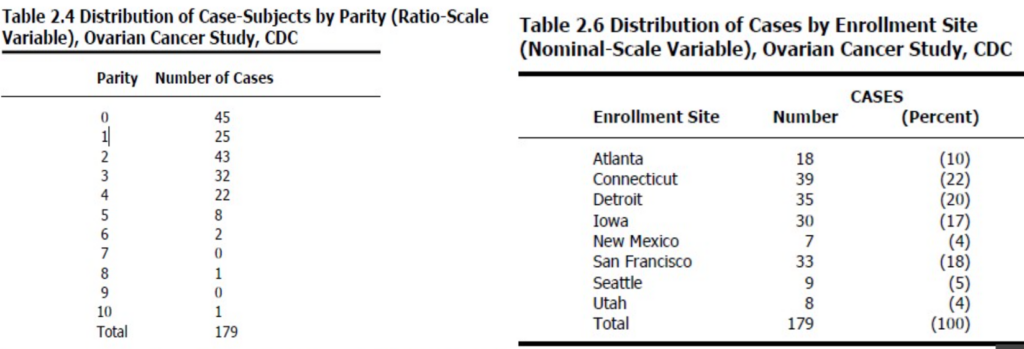
頻度分布の特性（Properties of Frequency Distributions）

  • 頻度分布のデータはグラフ化（graphed）できます。
  • グラフは3つの特徴を明らかにします：
    1. 分布がピークを持つ位置（central location）、
    2. ピークの両側でどれだけ広がっているか（spread）、
    3. ピークの両側で分布が対称的かどうか（whether it is more or less symmetrically distributed）。

中心位置（Central location）

  • このタイプの対称分布は、典型的なベル型曲線（bell-shaped curve）—または正規分布（normal distribution）としても知られています。
  • 特定の値での集中は、頻度分布の中心位置または中心傾向（central tendency）として知られています。
  • 分布の中心位置はその最も重要な特性の一つです。時には、分布全体を要約する単一の値として引用されることがあります。
  • 疫学で一般的に使用される中心位置の3つの尺度には、算術平均（Arithmetic mean）、中央値（Median）、および最頻値（Mode）があります。
  • より少なく使用される他の2つの尺度には、中点（Midrange）と幾何平均（Geometric mean）があります。

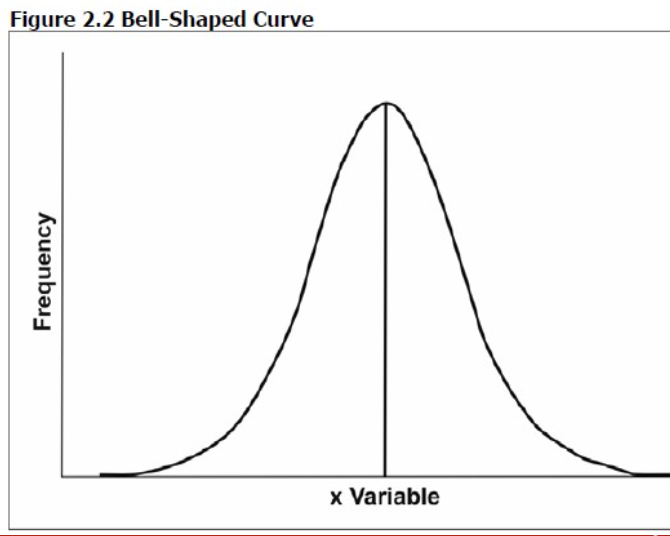
広がり（Spread、Variation、dispersion）

  • 同じ中心位置を持つが、異なる量の広がりを持っています。
  • 頻度の第二の特性としての広がりを指します。
  • 広がりは中心値からの分布を指します。
  • 疫学で一般的に使用される広がりの尺度には、範囲（range）と標準偏差（standard deviation）があります。
  • 頻度分布の広がりは、その中心位置とは独立しています。
  • 頻度分布は広がりの尺度を持つかもしれません。

形状（Shape）

  • 頻度分布の第三の特性です。
  • 人口の特性の頻度分布は対称的である傾向があります。
  • 非対称的、または一般に歪み（skewed）として知られています。
  • 歪みは山ではなく、尾を指します。したがって、左に歪んでいる分布は長い左の尾を持っていますと言われます。

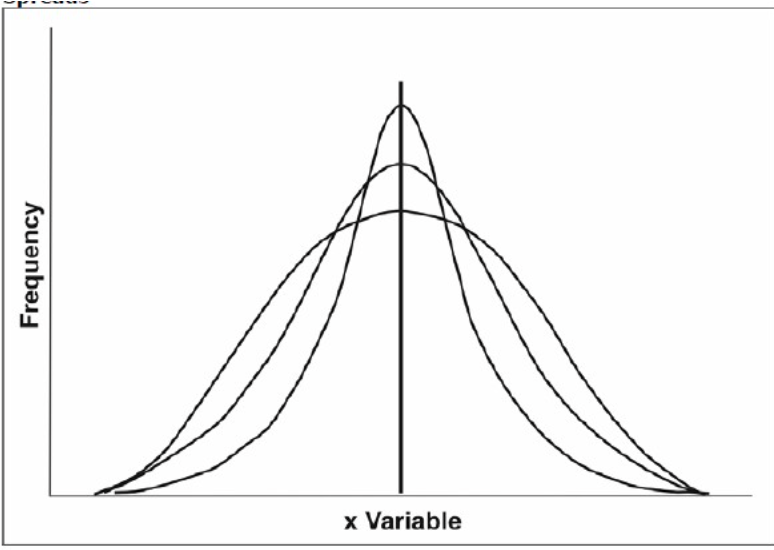
歪み（Skewness）

  • 中心位置が左側にあり、右側に尾が伸びている分布は、正の歪みまたは右側に歪んでいると言われます。
  • 中心位置が右側にあり、左側に尾がある分布は、負の歪みまたは左側に歪んでいると言われます。
  • 特に言及されるべき分布が一つあります—正規またはガウス分布（Normal or Gaussian distribution）。これは典型的な対称的なベル型曲線であり、数学的な方程式によって定義され、統計において非常に重要です。

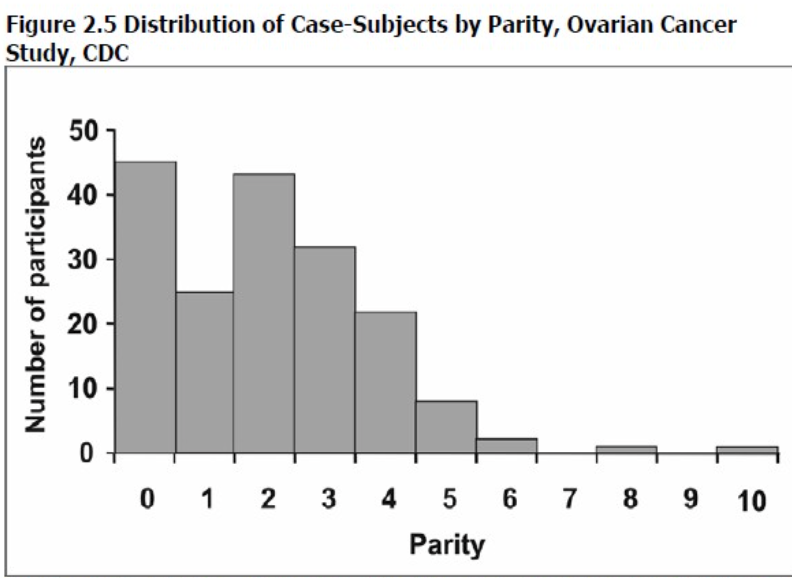
正規分布（Normal distribution、bell-shaped curve）

  • 正規分布は完全に対称であり、平均（mean）、中央値（median）、および最頻値（mode）はすべて同じ値を持ちます。
  • 平均 = 中央値 = 最頻値

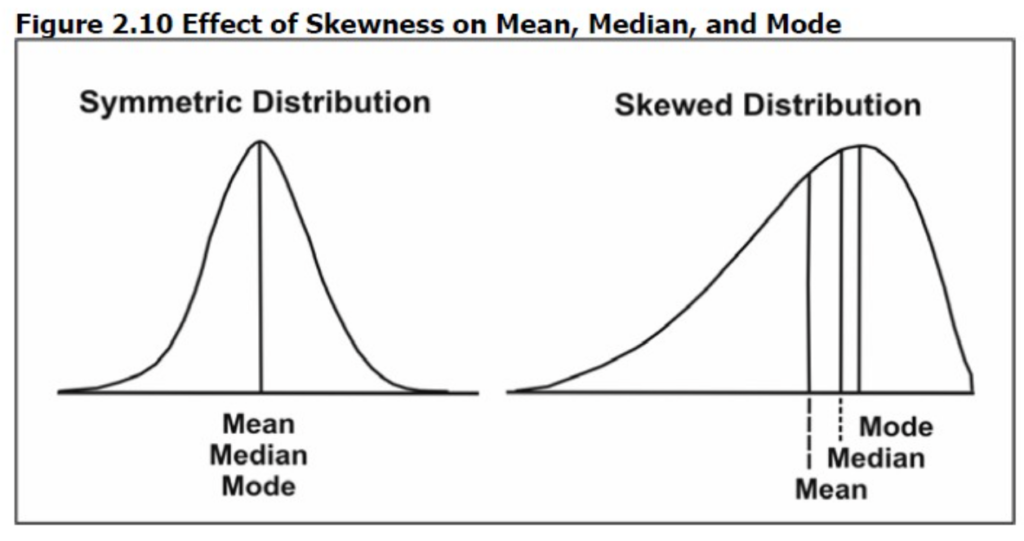
標準偏差（Standard deviation）

  • 平均とともに最も一般的に使用される広がりの尺度です。
  • 平均は中心位置の尺度として最も一般的に使用され、多くの統計テストと分析技術の基礎となっています。
  • 中央値の利点は、いくつかの非常に高いまたは低い観測値に影響されないことです。
  • データセットが歪んでいる場合、中央値は平均よりもデータを代表しています。

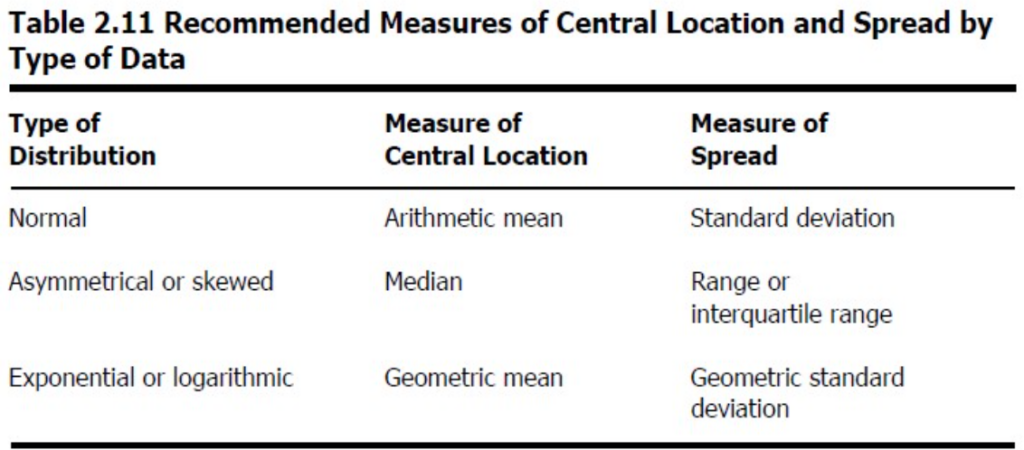
中心位置の尺度（Measures of Central Location）

  • データ分布全体を要約する単一の値を提供します。
  • それはデータ分布全体を最もよく代表する値です。
  • 中心位置の尺度には、最頻値（mode）、中央値（median）、算術平均（arithmetic mean）、中点（midrange）、および幾何平均（geometric mean）が含まれます。
  • 与えられた分布に使用する最適な尺度を選択することは、主に2つの要因に依存します：
    • 分布の形状または歪み（shape or skewness）、
    • 尺度の使用目的（intended use of the measure）。

最頻値（Mode）

  • データセットで最も頻繁に発生する値です。
  • 単純に各値が出現する回数を集計することで決定できます。
  • 2つ以上のモードがある場合：バイモーダル（Bi-modal）
  • 最頻値の特定方法：
    • ステップ1. 変数の値と各値の発生頻度を示す頻度分布に観察を配置します（または、DPTワクチンの投与回数のように少数の値のデータセットの場合、実際の値を昇順に配置します）。
    • ステップ2. 最も頻繁に発生する値を特定します。
  • データ例：特定の村の2歳児17人が受けたジフテリア-百日咳-破傷風（DPT）ワクチンの投与回数
    • データ: 0, 0, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4
    • 2人の子供が0回、2人が1回、3人が2回、6人が3回、4人が全4回の投与を受けました。
    • したがって、最頻値は3回の投与です。なぜなら、他のどの数よりも多くの子供が3回の投与を受けたからです。

最頻値の特性と使用法（Properties and uses of the mode）

  • 最頻値は理解しやすく説明しやすい中心位置の尺度であり、最も特定しやすい尺度でもあります。計算を必要としません。
  • 最も人気のある値や最も一般的な値について問題を解決するための中心位置の尺度として、最頻値が好まれます。これが「典型的な」数値です。
  • 分布が複数のモードを持つ場合、2つ以上の値が最も頻繁に発生する値としてタイになる場合です。値が1回以上現れない場合、モードは存在しません。
  • 最頻値はほぼ排他的に「記述的」尺度として使用されます。
  • 統計操作や分析ではほとんど使用されません。
  • 最頻値は、1つまたは2つの極端な値（外れ値）には通常影響されません。

中央値（Median）

  • ランク順に並べられたデータセットの中央値です。
  • 統計的には、中央値はデータを2つの半分に分ける値で、一方の半分の観測値は中央値より小さく、他方の半分は中央値より大きくなります。
  • 中央値はまた、分布の50パーセンタイルです。

以下は、肝炎Aの潜伏期間のデータを用いて中央値を求める例です。観測値の数が奇数の場合と偶数の場合の二つの例を示します。

例 A: 観測値の数が奇数の場合
肝炎Aの次の潜伏期間の中央値を見つけます：27日、31日、15日、30日、22日。

ステップ1. 値を昇順に並べる。
15日、22日、27日、30日、31日

ステップ2. 分布の中央位置を求める。
中央位置 = (n + 1) / 2 = (5 + 1) / 2 = 6 / 2 = 3 したがって、中央値は3番目の観測値になります。

ステップ3. 中央位置の値を特定する。
3番目の観測値 = 27日

例 B: 観測値の数が偶数の場合
肝炎Aの潜伏期間がさらに一つ報告されたと仮定します。この場合の潜伏期間は次の通りです：27日、31日、15日、30日、22日、29日。

ステップ1. 値を昇順に並べる。
15日、22日、27日、29日、30日、31日

ステップ2. 分布の中央位置を求める。
中央位置 = (n + 1) / 2 = 7 / 2 = 3.5 したがって、中央値は3番目と4番目の観測値の間の値になります。

ステップ3. 中央位置の値を特定する。
中央値は3番目（値 = 27日）と4番目（値 = 29日）の観測値の平均値です： 中央値 = (27 + 29) / 2 = 28日

中央値の特性と使用法（Properties and uses of the median）

  • 中央値は、特に歪んだ（skewed）データに対して良い記述尺度です。これは、分布の中心点であるためです。
  • 中央値は、最頻値（mode）と同様に、1つまたは2つの極端な値（outliers）に一般的に影響されません。
  • 中央値は比較的特定しやすく、観測値の数が奇数の場合は単一の観測値に等しく、偶数の場合は2つの観測値の平均に等しいです。
  • 中央値は理想的な統計的特性を持っていないため、統計操作や分析で使用されることはあまりありません。

算術平均（Arithmetic Mean）

  • 算術平均は、一般に平均（mean）またはアベレージ（average）と呼ばれるもののより技術的な名前です。
  • 算術平均は、分布内の他のすべての値に最も近い値です。
  • 算術平均の計算方法：
    • ステップ1. 分布内の観測値をすべて加算します。
    • ステップ2. 和を観測数で割ります。

算術平均の特性と使用法（Properties and uses of the arithmetic mean）

  • 平均は優れた統計的特性を持ち、追加の統計操作や分析で一般的に使用されます。
  • そのような特性の一つに、平均の中心化特性（centering property of the mean）があります。
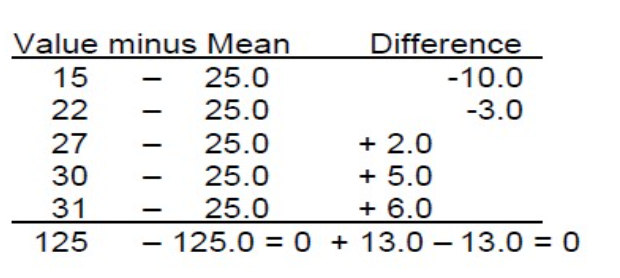
  • データセットの各観測から平均を差し引くと、これらの差の合計はゼロになります（つまり、負の合計は正の合計に等しいです）。
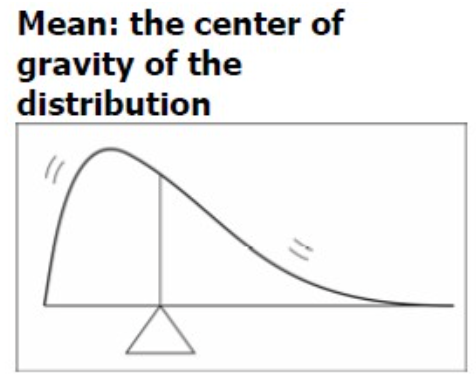
  • この中心化特性のために、平均は時に頻度分布の重心（center of gravity）と呼ばれます。
  • 算術平均は、通常分布したデータに対する最良の記述尺度です。
  • 平均は、極端に歪んだ（skewed）データや片方の方向に極端な値があるデータに対しては、選択の尺度とはなりません。

中点（Midrange）

  • 中点は観測のセットの中間点または中点です。中点は通常、他の尺度を決定する中間ステップとして計算されます。
  • 中点の特定方法：
    • ステップ1. 最小（minimum）観測と最大（maximum）観測を特定します。
    • ステップ2. 最小値と最大値を加算し、2で割ります。
  • 例外：年齢（age）は、最も近い整数に丸める通常のルールに従わないため、他の変数とは異なります。たとえば、17歳360日の人は少なくともあと5日間は18歳とは主張できません。したがって、年齢データの中点を特定するには、最小観測と最大観測を加算し、さらに1を加えて2で割る必要があります。
  • 中点（ほとんどのタイプのデータ） = (最小 + 最大) / 2
  • 中点（年齢データ） = (最小 + 最大 + 1) / 2

中点の特性と使用法（Properties and uses of the midrange）

  • 中点は中心位置の尺度として一般的に報告されることはありません。
  • 中点は他の計算の中間ステップや、区間で収集されたデータのグラフを作成する際により一般的に使用されます。

例 A: 肝炎Aの潜伏期間の中点を求める
潜伏期間: 27日、31日、15日、30日、22日

ステップ1. 最小値と最大値を特定する。
最小値 = 15, 最大値 = 31

ステップ2. 最小値と最大値を加えて2で割る。
中点（Midrange） = (15 + 31) / 2 = 46 / 2 = 23日

例 B: 1週間に消費されるアルコール飲料の数を表すグループ15-24の中点を求める
ステップ1. 最小値と最大値を特定する。
最小値 = 15, 最大値 = 24

ステップ2. 最小値と最大値を加えて2で割る。
中点 = (15 + 24) / 2 = 39 / 2 = 19.5

この計算は、グループ15-24が実際には14.50-24.49をカバーしていると仮定しています。14.50-24.49の中点は19.49…となり、中点は19.5と報告されます。

例 C: 年齢グループ15-24歳の中点を求める
ステップ1. 最小値と最大値を特定する。
最小値 = 15, 最大値 = 24

ステップ2. 最小値と最大値に1を加えて2で割る。
中点 = (15 + 24 + 1) / 2 = 40 / 2 = 20歳

これらの例では、データセットの最小値と最大値を用いて中点（Midrange）を計算しています。中点はデータセットの最小値と最大値の中間値を提供し、データの範囲の中心を示します。

標準偏差（Standard deviation）

  • 標準偏差は、算術平均（arithmetic mean）と共に最も一般的に使用される広がりの尺度です。
  • 平均（mean）から各観測値を差し引いて、その差の合計を加算すると0になります。
  • この標準偏差の概念は、平均から各観測を差し引くことが基本となります。
  • ただし、平均と各観測値の差は負の数を避けるために二乗されます。
  • 次にその平均を計算し、平方根を取って元の単位に戻します。標準偏巧の計算方法：
    • ステップ1. 算術平均を計算します。
    • ステップ2. 各観測値から平均を差し引きます。差を二乗します。
    • ステップ3. 二乗差の合計を求めます。
    • ステップ4. 二乗差の合計をn – 1で割ります。
    • ステップ5. ステップ4で得られた値の平方根を取ります。結果が標準偏巧です。

標準偏差の特性と使用法（Properties and uses of the standard deviation）

  • 標準偏差の数値は、統計的でない解釈が容易ではありませんが、他の広がりの尺度と同様に、観測が中心からどれだけ広がっているかまたは密集しているかを伝えます。
  • 標準偏差は、データがおおよそ「正規分布」している場合、つまりデータが典型的なベル型曲線に従っている場合にのみ計算されます。

肝炎Aの潜伏期間の平均と標準偏差の計算

ステップ1. 算術平均を計算する

平均 = (27 + 31 + 15 + 30 + 22) / 5 = 125 / 5 = 25.0日

ステップ2. 各観測値から平均を引き、その差を二乗する

値平均からの差差の二乗
2727 – 25.0 = +2.04.0
3131 – 25.0 = +6.036.0
1515 – 25.0 = -10.0100.0
3030 – 25.0 = +5.025.0
2222 – 25.0 = -3.09.0

ステップ3. 二乗差の合計を求める

合計 = 4 + 36 + 100 + 25 + 9 = 174

ステップ4. 二乗差の合計を(n – 1)で割る。これが分散です。

分散 = 174 / (5 – 1) = 174 / 4 = 43.5 (日の二乗)

ステップ5. 分散の平方根を取る。結果が標準偏差です。

標準偏差 = √43.5 ≈ 6.6日

この計算により、肝炎Aの潜伏期間データセットの平均と標準偏差が求められます。標準偏差はデータのばらつきを示す指標であり、平均からどれだけデータが散らばっているかを示します。

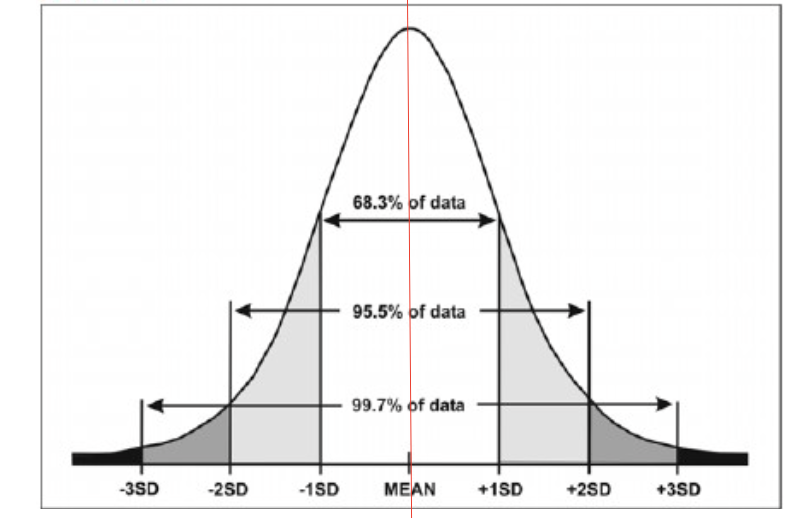
正規曲線下の面積と標準偏差1, 2, 3（Area Under Normal Curve within 1, 2, and 3 Standard Deviations）

  • 平均は中心にあり、データはこの平均の両側に等しく分布しています。
  • x軸に±1, 2, 3標準偏差がマークされます。
  • 正規分布データでは、約2/3（正確には68.3%）のデータが平均の両側1標準偏差内にあります；
  • 95.5%のデータが平均の両側2標準偏差内にあります；
  • 99.7%のデータが平均の両側3標準偏巧内にあります。
  • 正確に95.0%のデータが平均の1.96標準偏巧内にあります。

平均の標準誤差（Standard error of the mean）

  • 平均の標準誤差は、同じ人口から取られた繰り返しサンプルの算術平均に期待される変動性を指します。
  • 標準誤差は、持っているデータが実際にはより大きな人口からのサンプルであるという前提を持っています。
  • この前提によれば、あなたのサンプルは、ソース人口から取り得る無限の可能なサンプルのうちの1つにすぎません。したがって、あなたのサンプルの平均は、他の無限のサンプル平均のうちの1つにすぎません。
  • 標準誤差はこれらのサンプル平均の変動を定量化します。

平均の標準誤差の特性と使用法（Properties and uses of the standard error of the mean）

  • 平均の標準誤差の主な実用的な使用法は、算術平均周りの信頼区間を計算することです。

信頼限界（信頼区間）（Confidence limits, confidence interval）

  • 推論は、研究されているサンプルが全人口を代表しているという科学的一般化です。通常、推論には測定の精度についての何らかの考慮が含まれます。
  • 測定の精度を示す一般的な方法は、信頼区間を提供することです。
  • 狭い信頼区間は高精度を示し、広い信頼区間は低精度を示します。
  • 平均の信頼区間は、平均自体と標準誤差の何倍かに基づいています。

平均の95％信頼区間の計算方法（Method for calculating a 95% confidence interval for a mean）

  • ステップ1. 平均とその標準誤差を計算します。
  • ステップ2. 標準誤差に1.96を乗算します。
  • ステップ3. 95％信頼区間の下限 = 平均 – 1.96 x 標準誤差。
  • 上限 = 平均 + 1.96 x 標準誤差。
  • 一位に四捨五入すると、95％信頼区間は200.1から211.9です。言い換えれば、この研究の真の人口平均の最良の推定値は206ですが、200.1から211.9の範囲の値と一致しています。したがって、信頼区間は推定の精度を示します（この信頼区間は狭く、サンプル平均206はかなり正確であることを示します）。また、研究者がサンプルから全人口に推論を描く際の自信の程度も示します。

信頼区間の特性と使用法（Properties and uses of confidence intervals）

  • 平均だけでなく、信頼区間を計算すべきまたは計算されるべき他の尺度もあります。サンプル調査や研究からより大きな人口に推論を描く目的で、割合（proportions）、率（rates）、リスク比（risk ratios）、オッズ比（odds ratios）などの疫学的尺度に対しても一般的に信頼区間が計算されます。
  • ほとんどの疫学研究は、信頼区間の背後にある理論に必要な理想的な条件下で行われるわけではありません。
  • 平均、割合、リスク比、オッズ比などの尺度の信頼区間は、異なる式を使用して計算されます。
  • 信頼区間の解釈は常に同じです：区間が狭いほど推定が正確であり、区間内の値の範囲は研究からのデータと最も一致する人口値の範囲です。

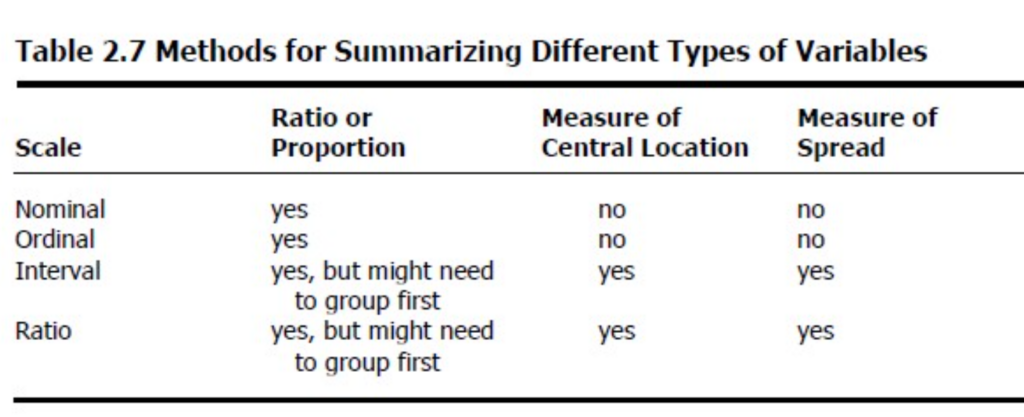
サンプリングの必要性（Why is sampling necessary in Research?）

  • この知識を使って簡単な例を挙げましょう：南アフリカの18〜24歳の被験者における甲状腺機能低下症の治療としてレボチロキシンの有効性をテストしたいとします。
  • 国内の甲状腺機能低下症を持つすべての個人を見つけ出し、そのデータを収集することは物理的に不可能です。
  • しかし、人口の代表的なサンプルを収集することができます。例えば、治療前後の甲状腺刺激ホルモン（thyroid stimulating hormone）レベルの平均（sample statistic）を計算することができます。
  • この平均を使用して、人口パラメータ（population parameter）についての結果を推測することができます。
  • この例では、甲状腺刺激ホルモンレベルは変数（variable）であり、各患者の実際の数値は個々のデータポイント（individual data points）を表します。

サンプリング（Sampling）

  • サンプルは、人口からの個体のサブセットです。
  • サンプリングは、実際にデータを収集するグループを選択することを意味します。
  • サンプリングにより、人口の特性についての仮説をテストすることができます。
  • 人口は、結論を引き出したい全体のグループです。
  • サンプルは、データを収集する特定の個体のグループです。
  • 人口は、地理的な位置、年齢、収入など、多くの異なる特性で定義することができます。

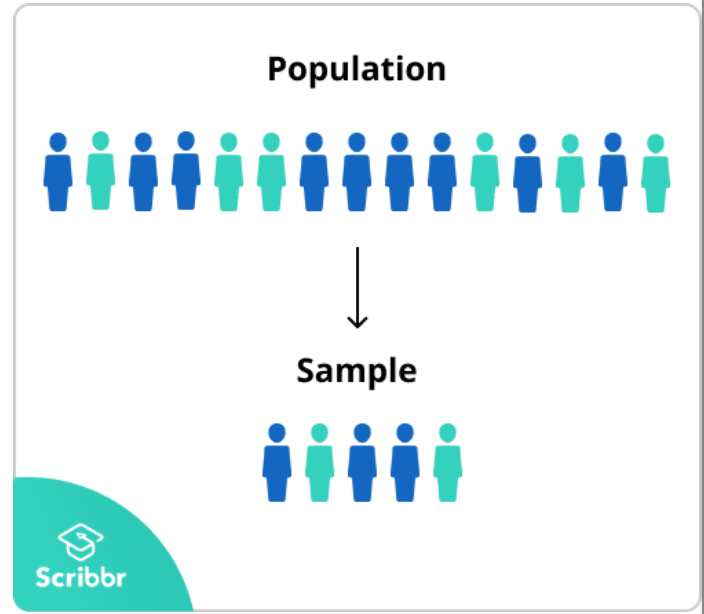
サンプリング方法の2種類（Two types of sampling methods）

  • 確率サンプリング（Probability sampling）はランダム選択を伴い、全体のグループについて統計的な推論を行うことができます。
  • 非確率サンプリング（Non-probability sampling）は便宜や他の基準に基づいた非ランダム選択を伴い、初期データを簡単に収集することができます。

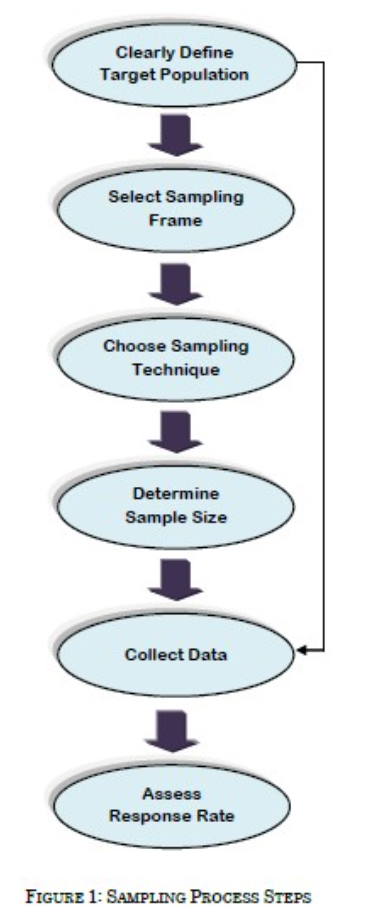
確率サンプリング方法（Probability sampling methods）

  • 確率サンプリング方法について詳しく説明するセクションです。

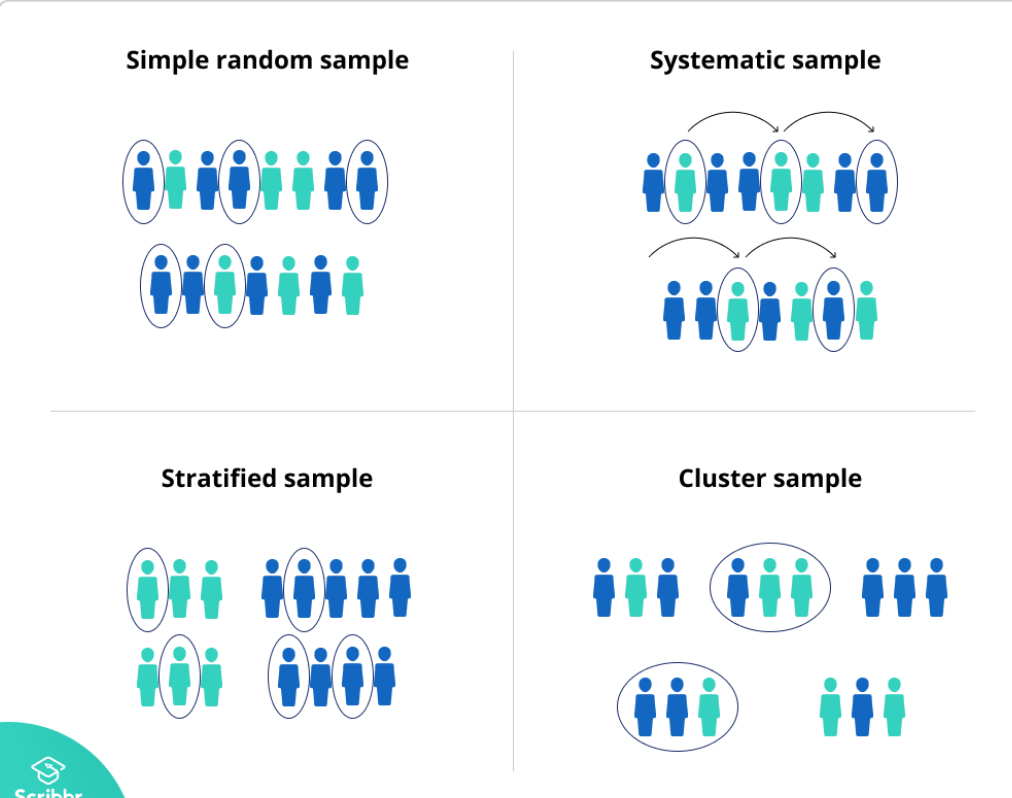
非確率サンプリング方法（Non-probability sampling methods）

  • 非確率サンプリング方法について詳しく説明するセクションです。

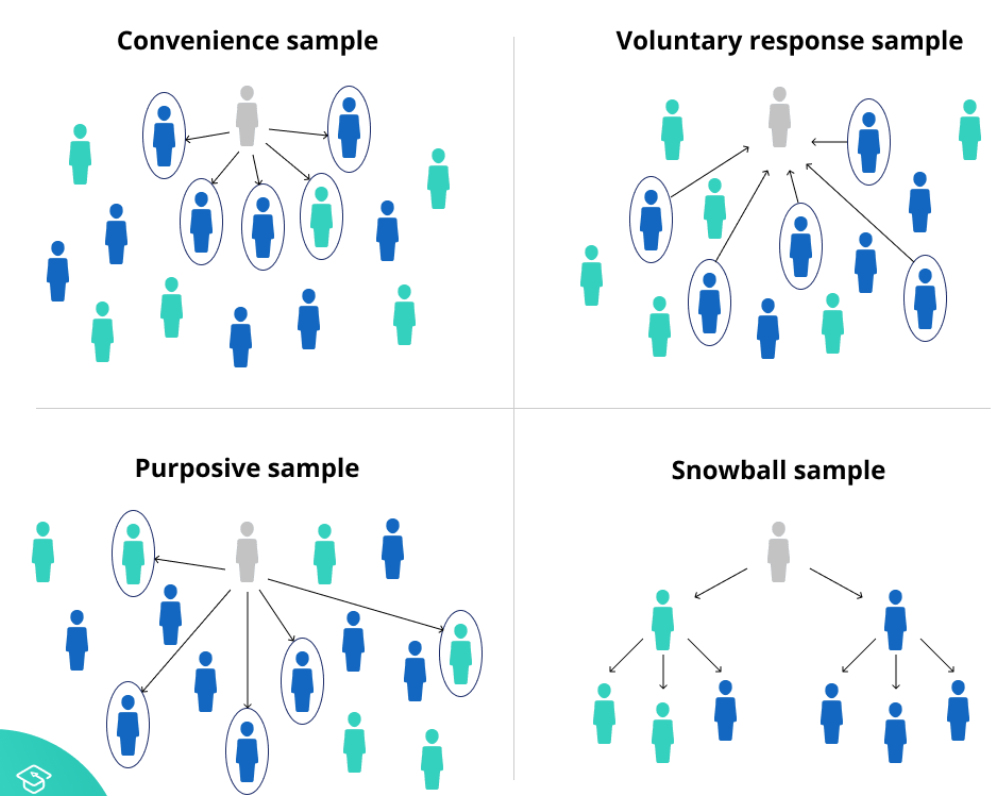
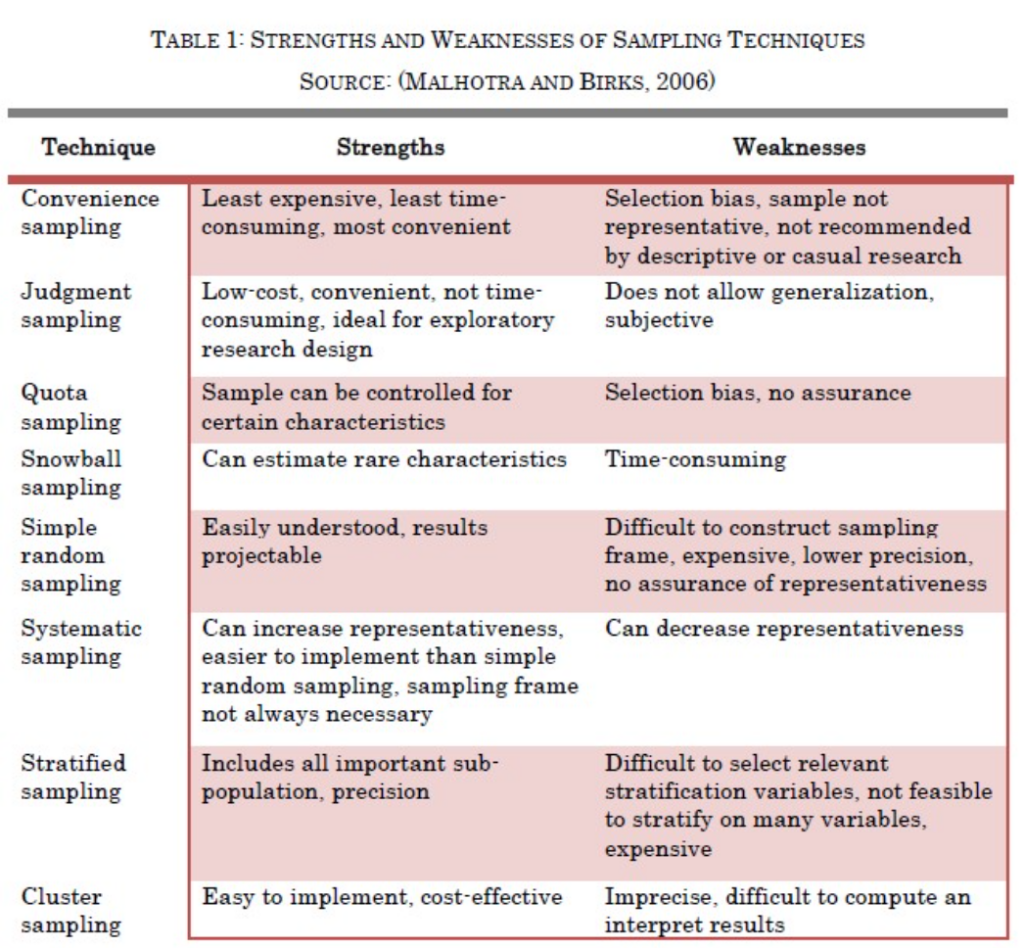
サンプルサイズ（Sample size）

  • ランダムサンプルから一般化するためには、ランダムサンプルが十分なサイズである必要があります。
  • 選択されたサンプルの絶対サイズは、人口の複雑さに対して相対的です。
  • サンプルが大きければ大きいほど、発見が偏っている可能性が低くなるというのは一般的ですが、サンプルが特定のサイズを超えると、迅速に減少するリターンが発生し、研究者のリソースとのバランスを取る必要があります。
  • 率直に言って、大きなサンプルサイズはサンプリングエラーを減らしますが、減少率は低下します。サンプルサイズを決定するためのいくつかの統計式が利用可能です。
  • カテゴリカルデータのサンプルサイズを計算するための多くのアプローチがあり、異なる式が組み込まれています。
  • n = p (100-p)z2/E2
    • n は必要なサンプルサイズ
    • P は状態または条件の発生割合
    • E は必要な最大誤差の割合
    • Z は必要な信頼レベルに対応する値

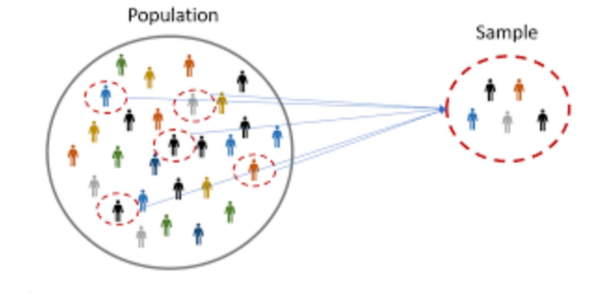
サンプリングバイアス（Sampling Bias）

  • サンプリングバイアスは、ある人口のメンバーが他のメンバーよりも系統的にサンプルに選ばれやすい場合に発生します。
  • バイアスの形態：
    1. 選択バイアス（Selection Bias）
    2. 非応答バイアス（Non-Response Bias、遅延応答）
    3. 応答バイアス（Response Bias）

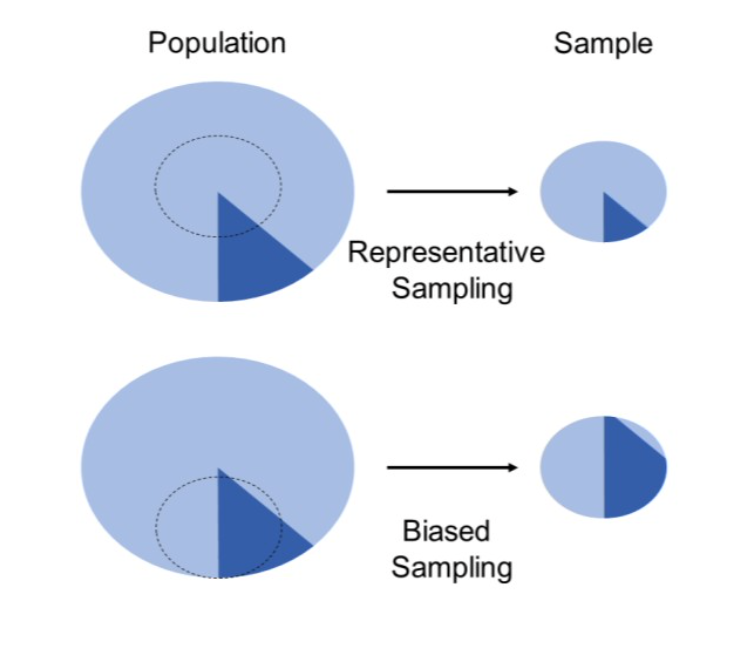
選択バイアス（Selection Bias）

  • 比較が、研究中のもの以外の結果の決定要因において異なる患者群間で行われる場合に発生します。
    1. 医学的監視バイアス（Medical Surveillance Bias）- 特定のグループが他のグループよりも頻繁に医者に行く（または診断テストを受ける）ため、関心のある病気の過検出が発生します。
    2. 中心集中バイアス（Centripetal Bias）- 主要な臨床センターが特定の臨床医学分野における専門知識によって部分的に評価される場合、その専門知識から恩恵を受けそうな問題例を紹介されることがあります。
    3. 人気バイアス（Popularity Bias） – 専門家がこれらのケースを他の挑戦的でないまたは興味深くないケースよりも優先的に受け入れ、追跡する場合があります。
    4. 紹介フィルターバイアス（Referral Filter Bias） – 紹介プロセスの各段階で発生する選択により、三次ケアセンターでの患者サンプルが一般人口とは大きく異なることがあります。
    5. 診断アクセスバイアス（Diagnostic Access Bias） – 患者が研究の対象として適格であると識別される臨床技術への財政的および地理的アクセスが異なります。
    6. バークソンバイアス（Berkson Bias） – 病院から選ばれた研究人口は、一般人口よりも健康状態が悪い可能性があります。

サマリー（Summary）

  • 中心位置の尺度は、分布の観測値を要約する単一の値です。
  • 最頻値は最も一般的な値を提供し、中央値は中心値を提供し、算術平均は平均値を提供し、中点は中間値を提供します。
  • 最頻値と中央値は記述的尺度として有用ですが、さらなる統計的操作にはあまり使用されません。
  • 対照的に、平均は良い記述的尺度であり、良好な統計的特性を持っています。平均は追加の統計操作で最も頻繁に使用されます。
  • 最小値と最大値に基づいている中点は、他の尺度よりも外れ値に敏感です。
  • サンプルは、より大きな人口からの個体のサブセットです。
  • サンプリングは、研究で実際にデータを収集するグループを選択することを意味します。
  • 統計学では、サンプリングを使用して人口の特性に関する仮説をテストします。
  • サンプルは人口についての推測を行うために使用されます。サンプルは実用的で、コスト効果が高く、便利で、管理が容易なため、データを収集するのが容易です。
  • 確率サンプリングでは、対象人口の各メンバーがサンプルに含まれる確率が既知です。
  • 非確率サンプリングでは、サンプルは非ランダム基準に基づいて選択され、人口のすべてのメンバーがサンプルに含まれる可能性はありません。

Lesson 7：Sources of Data in Public Health

一般的な目標（General objectives）

  1. 定例の公衆衛生情報システム（Routine and Public health information systems）を定義し、説明する
  2. 公衆衛生情報の3タイプを知る
  3. 健康記録システム（Health Record Systems）の利点と制限を知る
  4. 健康システムの効果とパフォーマンスを監視するためのLGUスコアカード（LGU-Scorecard）に精通する

概要（Overview）

  • 疫学（Epidemiology）は、発生期間、場所、関与する人々などのイベントを監視、調査、評価する上で重要な役割を果たします。健康データソースは、病気の傾向を特定したり、病気のパターンを研究して問題を優先順位付けするために必要な生の情報を提供することで重要です。これにより、政策立案者は健康プログラムを計画し、介入して解決策を提供するための措置を実行することが可能になります。
  • 記述疫学（Descriptive epidemiology）は、データを整理し分析することで病気と宿主の個人的特性（person, place, and time）を理解する方法を提供します。
  • リスク（risk）と負担（burden）の尺度は、政府がプログラムを展開するための多くの健康政策と計画の基盤となっています。これらの主な目的は問題の規模を減少させることです。立法は多数派に影響を与える病気や問題によって影響を受けます。

健康情報システム（Health information system）

  • 健康情報システムには3つのタイプがあります：
    1. 市民登録または生命登録システム（Civil or vital registration system）- 例：出生証明書（Birth certificate）、死亡証明書（Death certificate）、結婚証明書（marriage certificate）
    2. 医療記録システム（Medical records system）- 例：患者のチャート（patient’s chart）
    3. 行政記録システム（Administrative records system）- 例：国勢調査（Census）、メディケア（Medicare）

健康指標（Indicators of Health）

  • 死亡率（Mortality）
  • 罹患率（Morbidity）
  • 出生率（Natality）
  • 障害（Disability）
  • 栄養状態指標（Nutritional status indicators）
  • 医療提供指標（Health care delivery indicators）
  • 利用指標（Utilization indicators）
  • 社会および精神健康指標（Indicators of social and mental health）
  • 環境保健指標（Environmental health indicators）

人口指標（Demographic indicators）

  • 人口学（Demography）は、出生（births）、死亡（deaths）、移住（migration）の相互作用によって引き起こされる変化と関連して人口を研究します。
  • 死亡率（Mortality）
  • 罹患率（Morbidity）
  • 障害（Disability）
  • 出生率（Natality）
  • 人口統計（Population statistics）（人口規模（Population size）、密度（Density）、性比（sex ratio）、依存率（dependency ratio））
  • 生命統計（Vital statistics）（出生率（Birth rate）、死亡率（Death rate）、成長率（Growth rate）、出生時の平均寿命（life expectancy at birth）、死亡率および出生率（Mortality and fertility））

公衆衛生におけるデータソース（Data Sources in Public Health）

  • 健康情報システムは通常のデータを定期的に収集しますが、これらのシステムが収集するデータは人口の死亡率（mortality）や罹患率（morbidity）に関する情報を提供します。
  • 定例の健康情報システム（Routine health information systems）は、人口健康の他の測定データを提供する点で不足があります。ここで、公衆衛生情報システム（Public Health Information Systems）やその他の特別に設計された研究が公衆衛生問題を解決する際により良い利益を提供します。
  • 定例の健康情報システムは、意思決定に使用できるタイムリーな情報を生成することができます。たとえば、データ健康情報システムは、重要な公衆衛生目標に向けた進捗を監視するためによく使用されます。そのような目標には、ミレニアム開発目標（Millennium Development Goals）などがあります。

健康情報システム（RHIS）- 定例（Routine Health Information Systems）

  • 定例健康情報システムは、意思決定のためのタイムリーで質の高い情報を生成します。
  • RHISのデータは、目標達成の進捗を監視するために使用されます。これには以下が含まれます：
    • ミレニアム開発目標（Millennium Development Goals）およびその先
    • 人々の健康（Health of the People）（スコアカードシステム）
  • 伝統的なRHISには、以下が含まれます：
    • 市民登録および生命統計システム（Civil registration and vital statistics systems）
    • 医療記録システム（Medical record systems）
    • 行政記録システム（例：国勢調査、メディケア）（Administrative record systems, e.g., Census, Medicare）

生命統計と人口統計（VITAL STATISTICS AND DEMOGRAPHICS）

  • 生命統計は、数値的な記述を扱うバイオメトリー（biometry）の一部です。
  • 生命登録システム（Vital registration systems）は、生命統計にとって最高のデータを提供します。
  • 生命統計は重要で、研究者、疫学者（epidemiologist）、保健計画者（health planners）、その他の保健専門家にとって以下のような目的で使用されます：
    1. コミュニティの健康状態を判定する（to determine the health status of a community）
    2. どのように最善の保健サービスを提供するか決定する（to decide how best to provide a health service）
    3. 公衆衛生プログラムを計画する（to plan a public health program）
    4. プログラムの効果を評価する（to evaluate a program’s effectiveness）
  • 人口統計（Demographic）は、人口の特性を説明する変数です。

生命登録システム（Vital Registration systems）

  • 生命記録（Vital Records）:
    • 「出生、死亡、結婚、離婚の証明書は、法的および人口統計の目的で必要とされる。文字通り、生きていることに関連する記録です。」
    • 国内登録（Country Registry、完全な生命登録システム）: 国家がこれらの記録を保持します。
    • 国家登録（National registry）もこれらの記録から収集されたデータの一部を受け取ります。
    • 世界的に（World-wide）:
      • 記録は地方、州、または連邦レベルで保持されることがあります。
    • 生命登録システムは、生命統計が推定されるデータをキャプチャするために特別に開発されたシステムです。これは市民登録システムが存在しない場合に最も頻繁に発生します。
    • 現在よく使用される用語は市民登録システム（civil registration system）と生命統計（vital statistics）です。なぜなら、システムがデータを収集するメカニズムであり、そこから生命統計を推定することができるからです。

生誕証明書（Birth Certificate）のために収集される基本データ

  • 赤ちゃん（Baby）:
    • 生年月日（Date of birth）
    • 出生地（Place of birth）- 国籍を確立する（establish nationality）
    • 性別（Sex）
  • 母親（Mother）:
    • 生年月日（Date of birth）
    • 人種/民族（Race/ethnicity）
    • 居住地（Residence）
    • 出産時の婚姻状態（Marital status at time of delivery）
  • 父親（Father）:
    • 生年月日（Date of birth）
    • 人種/民族（Race/ethnicity）
    • 居住地（Residence）

死亡証明書（Death Certificate）のために収集される基本データ

  • これらのデータは国際疾病分類第10版（International Classification of Disease version 10、ICD-10）コードを使用して収集されます。

市民登録システムからのデータの正確性（Accuracy of Data from Civil Registration Systems）

  • カバレッジ（Coverage）
    • 死因の医療認証を受けた人口の割合
  • 完全性（Completeness）
    • 医療認証された死因の割合
  • 欠損データ（Missing data）
    • 年齢、性別、人種データが欠けている死因報告の割合
  • あいまいなカテゴリの使用（Use of ill-defined categories）
    • 様々な雑多なあいまいなカテゴリに分類された死亡の割合
  • 不可能な分類（Improbable classifications）
    • 信じがたい年齢や性別のカテゴリに割り当てられた死亡数、10万件の死亡コードあたり
  • 死因と一般死亡率の一貫性（Consistency between cause of death and general mortality）
    • 死因データポイントが一般死亡率に基づく予測から2（または3）標準偏差以上逸脱する割合

医療記録システム（Medical Record Systems）

  • これらのデータは、患者の臨床管理のために収集されます。
  • これは公衆衛生問題を調査するためのデータ収集と同じ目的ではありません。
  • 医療記録のデータ収集方法について考えてみてください。
    • 医師からのテキスト
    • 内部および外部の研究室からのラボ値
    • テストの注文と薬の処方
    • 診断の除外

医療記録データの使用時の課題（Challenges When Using Medical Record Data）

  • 結果はしばしば外部ソースでの検証が必要です。
    • 死亡登録（Death registries）
    • がん登録（Cancer registries）
  • 診断コードや手順コードの変更を考慮する必要があります。
  • しばしば医療記録システムは単一の病院設定で一貫して使用されていません。
  • 電子医療記録はしばしば請求に焦点を当てています。
  • 医療記録システムが電子的でない場合：
    • データの電子形式への入力時の筆記問題
    • 記録の欠落
    • データを使用可能な形式に変換するための抽象化とコーディング

医療記録データの制限（Limitations to Medical Record Data）

  • 測定（Measurement）
    • 行動データは通常利用できません。
    • 情報が収集されるタイミング（例：医師がすべての訪問で必ずしも喫煙状態を記録しない）
    • 他の場所でケアを受けた場合、データが完全ではない可能性があります。
  • 研究対象人口（Study population）
    • 医療を受けている人々のみを捉えます。

行政記録システム（Administrative Record Systems）

  • このデータは、人口の病気の負担に洞察を提供するのに非常に役立ちます。
  • 公衆衛生で一般的に使用される行政記録の情報源：
    • 国勢調査（Census）
    • 政府が後援する健康プログラム（例：メディケイド＆メディケア）（Government-sponsored health programs, e.g., Medicaid & Medicare）
    • 保険/製薬データベース（私的）（Insurance/Pharmaceutical databases (private)）
  • 健康統計で一般的に使用される行政記録：
    • 人口の基数を決定する国勢調査データ（Census data）

行政記録の使用時の課題（Challenges When Using Administrative Records）

  • このデータは行政目的のために収集され、公衆衛生または統計生成目的のためではありません。
  • このデータの使用に関連する障害があります。
    • アクセス – データを利用可能にする義務は通常ありません。
    • 財政的コスト（Financial costs）
    • 時間コスト（データの申請、アクセスの取得、データの使用方法のトレーニング）（Time costs (applying for the data, gaining access, training as to how to use the data)）

行政記録データの制限（Limitations to Administrative Record Data）

  • 測定（Measurement）
    • 行動データは通常利用できません。
    • 情報が収集されるタイミングが一貫していない可能性があります。
    • 行政/請求コードの使用（Use of administrative/billing codes）
  • 研究対象人口（Study population）
    • 給付を受けている人々のみを捉えます。

地方自治体のスコアカード（Local Government Unit Scorecards）

  • LGUスコアカード（LGU-SC）は、公平性と効果の監視と評価（Monitoring and Evaluation for Equity and Effectiveness, ME3）の一環です。
  • これは、自治体、市、県内のクライアントや公私のプロバイダーを含む県全体の保健システム（province-wide health system, PWHS）のステークホルダーの組み合わせた努力のパフォーマンス評価です。

LGUスコアカードの報告または評価システム（Reporting or Grading System in LGU Scorecards）

  • これは、地方自治体（LGUs）が健康部門の改革のために求められる結果を実現し、国家の健康目標を達成する進捗を評価するためのパフォーマンスを測定し追跡します。

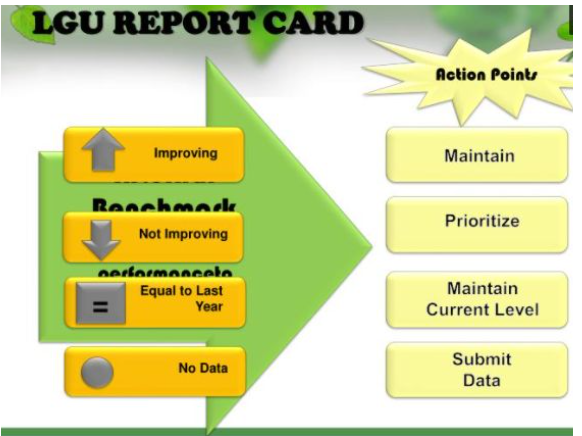
LGUの健康パフォーマンス指標（Health Performance Indicator of LGU）

  • LGUスコアカードは、健康部門の改革のために求められる結果を実現するための地方自治体のパフォーマンスを追跡するために意図されています。
  • 緑色は優れており、PWHSのパフォーマンスは2010年の目標と同等またはそれ以上です。黄色は良好で、PWHSのパフォーマンスは2006年の基準値以上ですが、2010年の国家目標よりも低いです。赤色はまあまあで、PWHSのパフォーマンスは2006年の基準値よりも低いです。

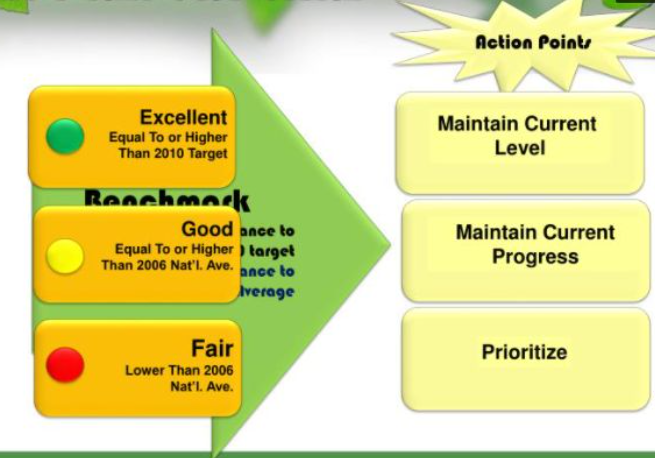
スコアカードのデータソース（DATA sources for the Scorecards）

  • スコアカードの成果は、外部および内部の目標に対してベンチマークされます。PWHS外部ベンチマークの結果。これにより、LGUとステークホルダーは、2006年の全県の平均パフォーマンスと国際および国家の基準と比較して自らのパフォーマンスをベンチマークするのに役立ちます。外部ベンチマークは、県の保健システムが国家目標にどれだけ近いか、また他の県の進捗と比較してどうかを決定します。一方、内部ベンチマークは、県のパフォーマンスが改善しているかどうかを判断します。両方のベンチマークは、県が行動を起こす必要がある場所についての推奨を行います。LGUスコアカードは、参加する県のパフォーマンスのレベルに対応する色を割り当てます。

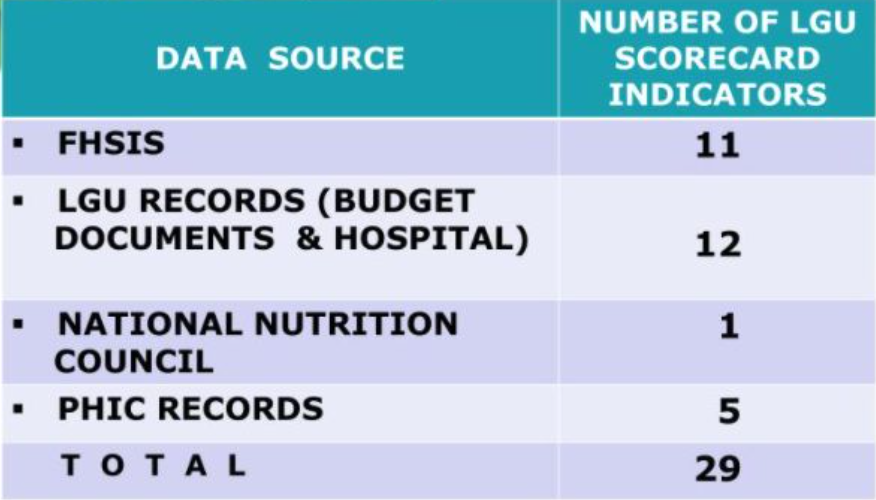
データプロセス（Data Process）

公衆衛生情報システム（PHIS）（Public Health Information Systems）

  • 伝統的なソース：
    • 人口ベースおよびトピック指向の調査（Surveys that are population-based and topic-oriented）
    • 特定の健康結果の登録簿（Registries of specific health outcomes）
    • 監視システム（Surveillance systems）
  • これらのデータは、死亡率や定例統計を超えた健康統計のためのデータを提供します。これらのデータは、通常の公衆衛生目的（usually specific public health purpose）のために収集されるため、市民/生命登録データと比較して目的に富んだものです。

A. 人口ベースの調査（Population-based Surveys）

  1. 地元の調査：例えば、市/町/クラス/セクション/レベル
    • バランガイ（Brgy…）のゴミ処理実践
  2. 国家レベル（National）：
    • 国民健康栄養調査（National Health and Nutrition Examination Survey, NHANES）
  3. 国際レベル（International）：多くの国々で使用される調査
    • 世界保健調査（World Health Survey）
    • 人口と健康調査（Demographic and Health Surveys, DHS）
  4. 人口と健康調査：
    • これらの調査は、自己報告された健康行動を測定します。
    • 一部は検体も採取します。
    • セブ市のHCWの精神健康状態を評価します。

B. 登録簿（Registries）

  • 登録簿は特定の疾患の結果に関するデータを収集します。
  • 登録簿は「ケース」のみを含みます。
  • 登録簿は特定の結果のために設計されているため、データは豊富です。
  • 例：AB型（-）登録簿、HIV/AIDS登録簿
  • 例

C. 監視システム（Surveillance system）

  • 監視は「データの体系的かつ連続的な収集、分析、解釈であり、適時かつ一貫した結果の普及と評価と密接に統合され、知る権利を持つ人々に行動がとられるようにすることです。これは疫学および公衆衛生実践の本質的な特徴です。」（Porta 2014）
  • 監視データの例
    • FluView：CDCのインフルエンザ監視
    • WorldometerでのCOVID-19

概要（Summary）

  • 記述疫学は、人、場所、時間の変数に応じて病気の発生を分類します。
  • 記述疫学研究は、解析疫学研究によって探求される仮説を生成するのに役立ちます。
  • 記述疫学は、介入の設計のために優先されるべき健康結果を示します。
  • 人の変数には、性別、年齢、人種/民族、経済状態が含まれます。
  • 場所の変数には、国際的、国内的、都市-農村、局地的パターンのタイプの比較が含まれます。
  • 時間の変数には、長期的傾向、周期的傾向、ポイントエピデミック、クラスタリングが含まれます。
  • 記述疫学は疫学推論のプロセスの重要な構成要素です。
  • 健康結果は、措置や特定の保健ケアの投資または介入から生じる健康の変化です。
  • 健康指標は、人または人口の健康状態を反映する測定可能な変数です。
  • 健康指標は健康の側面を反映します。
  • 健康決定要因は健康に影響を与える測定です。これには食事、喫煙、水質、収入、保健サービスへのアクセスが含まれます。
  • 健康情報システムには3タイプがあります：市民または生命登録システム（Civil or vital registration system）、医療記録システム（Medical records system）、行政記録システム（Administrative records system）。

概要（Summary）

  • 公衆衛生の意思決定は定量的な問題です。
  • 人口の健康は、その生命統計と人口統計データを使用して評価されます。人口特性に関する情報は、国勢調査データ、生命事象の登録、罹患調査から入手可能です。
  • このようなデータは、健康問題の規模を示すために使用される生命率やその他の統計を計算するために使用されます。
  • 生命率、比率、比は死亡（death）、出生（birth）、罹患（illness）の尺度に分類されます。
  • これらの尺度は粗（crude）または特定（specific）のものであり、後者は年齢、性別、人種、病気の経験などの共通の特徴を持つサブグループの計算を指します。
  • 異なる人口間の生命率、比率、比の比較は慎重に行われ、特定または調整された尺度を使用して検証されるべきです。
  • 調整方法の選択は利用可能なデータのタイプに依存します。

コメント